User:Matteo.focardi/sandbox

2020 Mathematics Subject Classification: Primary: 28A [MSN][ZBL]

A theorem on the relation between the concepts of almost-everywhere convergence and uniform convergence of a sequence of functions. Let $\mu$ be a $\sigma$-additive measure defined on a $\sigma$-algebra ${\mathcal A}$, let $E\in{\mathcal A}$, $\mu(E)<+\infty$, and let $f_kE\to\mathbb{R}$ be a sequence of $\mu$-measurable functions converging $\mu$-almost-everywhere to a function $f$. Then for any $\varepsilon>0$ there exists a measurable set $E_\varepsilon\subset E$ such that $\mu(E\setminus E_\varepsilon)<\varepsilon$, and the sequence $f_k$ converges to $f$ uniformly on $E_\varepsilon$. The case of the Lebesgue measure on the line was first proved by D.F. Egorov [1]. Note that the result is in general false if the measure $\mu$ is only $\sigma$-finite. A typical application is when $\mu$ is a positive Radon measure defined on (cf. Measure in a topological vector space) defined on of a topological space $X$ and $E$ is a compact set.

Egorov's theorem has various generalizations. For instance, to measurable mappings defined on a locally compact space $X$ valued into a metrizable space $Y$. The conclusion of Egorov's theorem may be false if $Y$ is not metrizable.

References

[1]	D.F. Egorov, "Sur les suites de fonctions mesurables" C.R. Acad. Sci. Paris , 152 (1911) pp. 244–246
[2]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801
[3]	N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) MR0583191 Zbl 1116.28002 Zbl 1106.46005 Zbl 1106.46006 Zbl 1182.28002 Zbl 1182.28001 Zbl 1095.28002 Zbl 1095.28001 Zbl 0156.06001

Comments

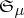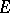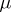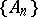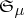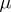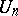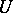In 1970, G. Mokobodzki obtained a nice generalization of Egorov's theorem (see [a2], [a3]): Let , and be as above. Let be a set of -measurable finite functions that is compact in the topology of pointwise convergence. Then there is a sequence of disjoint sets belonging to such that the support of is contained in and such that, for every , the set of restrictions to of the elements of is compact in the topology of uniform convergence.

Egorov's theorem is related to the Luzin -property.

References

[a1]	P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802
[a2]	C. Dellacherie, P.A. Meyer, "Probabilities and potential" , C , North-Holland (1988) (Translated from French) MR0939365 Zbl 0716.60001
[a3]	D. Revuz, "Markov chains" , North-Holland (1975) MR0415773 Zbl 0332.60045