Lax-Milgram lemma

Many boundary-value problems for ordinary and partial differential equations can be posed in the following abstract variational form (cf. also Boundary value problem, ordinary differential equations; Boundary value problem, partial differential equations): Find 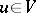such that

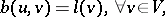(a1)

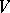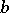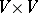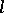where is a normed linear space (cf. also Norm), denotes a functional on and is an element in 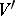(the dual of ).

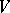The essential question here is what conditions can be imposed on 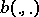and the normed space 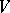so that a unique solution to (a1) exists and depends continuously on the data .

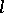The first result in this direction was obtained in 1954 by P.D. Lax and A.N. Milgram [a1], who established sufficient conditions for the existence and uniqueness of the solution for (a1).

Let 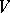be a reflexive Banach space (cf. also Reflexive space) and let $b:V\times V\longrightarrow\mathbb{C}$ be a sesquilinear mapping (bilinear when 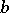is real; cf. also Sesquilinear form) such that

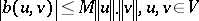(continuity) and

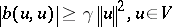(strong coercivity), where 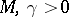. Then there exists a unique bijective linear mapping 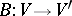, continuous in both directions and uniquely determined by 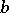, with

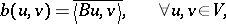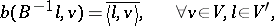and for the norms one has:

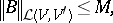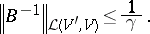This implies that 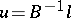is the solution of (a1). The above theorem only establishes existence of a solution to (a1), namely 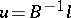, but does not say anything about the construction of this solution. In 1965, W.V. Petryshyn [a2] proved the following result: Let 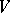be a separable reflexive Banach space (cf. also Separable space), 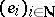a basis of and 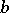a continuous sesquilinear strongly coercive mapping on 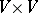. Then for all :

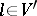i) for all 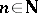the system

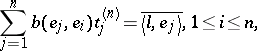is uniquely solvable for ;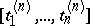

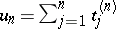ii) the sequence determined by converges in 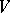to a that is the solution of (a1).

To see that the strong coerciveness property of the sesquilinear mapping 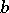is not necessary for the existence of the solution to (a1), consider the following very simple example.

Let 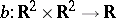be defined by

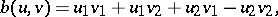where 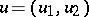, 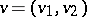. It is easy to see that 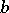is bilinear and continuous. It is not strongly coercive, because when 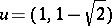. However, for all ,

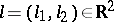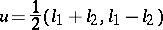is the unique solution to (a1).

In 1971, I. Babuška [a3] gave a significant generalization of the Lax–Milgram theorem using weak coerciveness (cf. Babuška–Lax–Milgram theorem).

An extensive literature exists on applications of the Lax–Milgram lemma to various classes of boundary-value problems (see, e.g., [a4], [a5]).

References

[a1]	P.D. Lax, A.N. Milgram, "Parabolic equations" Ann. Math. Studies , 33 (1954) pp. 167–190
[a2]	W.V. Petryshyn, "Constructional proof of Lax–Milgram lemma and its applications to non-k-p.d. abstract and differential operator equation" SIAM Numer. Anal. Ser. B , 2 : 3 (1965) pp. 404–420
[a3]	I. Babuška, "Error bound for the finite element method" Numer. Math. , 16 (1971) pp. 322–333
[a4]	J.T. Oden, J.N. Reddy, "An introduction to the mathematical theory of finite elements" , Wiley (1976)
[a5]	J. Nečas, "Les méthodes directes dans la théorie des équations elliptiques" , Masson (1967)