User:Yakovenko/sandbox1
Connection
$\def\G{\varGamma}$
An infinitesimal structure on a (smooth) bundle which allows to define the parallel transport between fibres of the bundle.
Historical overview
Initially the notion of connection appeared in the works by Gregorio Ricci and Tullio Levi-Civita who constructed the infinitesimal parallel transport between tangent spaces of a Riemannian manifold. Later the construction was distilled from the Riemannian context by Éli Cartan who constructed connections on principal bundles (equipped by action of a Lie group) and introduced the notion of the connection form. Finally, Charles Ehresmann gave a general definition of connection via distribution of horizontal subspaces, which is the most general construction using only the smooth structure and local triviality of the bundle.
In practice when dealing with connections, one distinguishes several particular cases of bundles and several (interrelated) ways to describe the infinitesimal parallel transport.
- Connections on the vector bundles, defined by an operator of covariant derivation;
- Affine connections on manifolds, defined on the tangent (and cotangent) bundle to a smooth manifold;
- Connections on $G$-bundles equipped with fibrewise action of a Lie group $G$;
- Levi-Civita (metric) connections on Riemannian manifolds, defined on the tangent bundle and preserving the metric structure.
Ehresmann connection
Let $\pi:E\to B$ be a smooth bundle with a generic fiber $F$. The Ehresmann connection is a "horizontal" subbundle $\G\subset TE$ of the tangent bundle, complementary to the "vertical" subbundle $\operatorname{Ker}\rd \pi$. In other words, the tangent space $T_xE$ at any point $x\in E$ is split as a direct sum of the vertical subspace $V_x=T_x F_x$ tangent to the fiber $F_x=\pi^{-1}(\pi(x))$ through $x$, and a complementary subspace $\G_x\subset T_x$; by definition of complementarity, $\dim\G_x=\dim B$, and the restriction $\rd \pi(x)|_{\G_x}\to T_{\pi(x)}B$ is an isomorphism.
This splitting allows to define the parallel transport along any smooth curve $\gamma:[0,1]\to B$ between the fibers $F_0=\pi^{-1}(\gamma(0))$ and $F_1=\pi^{-1}(\gamma(1))$ as follows. Consider the induced bundle $\pi'=\gamma^*\pi$ over the new base $B'=[0,1]$: because of the triviality of the segment $[0,1]$, this bundle is trivial, with the total space $E'\simeq F\times [0,1]$, and the horizontal subbundle $\G$ induces a horizontal subbundle $\G'=\gamma^*\G$ on $E'$. But since the base is now one-dimensional, the distribution $\G'$ is integrable and defines the foliation on $E'$, everywhere transversal to the fibers. Under mild additional conditions[1] the leaf (integral trajectory of the integrable distribution $\G'$) passing through the point $x\in F_0=F\times\{0\}$, crosses the fiber $F_1=F\times\{1\}$ at a unique point $\tau_0^1(x)\in F_1$. By the general theorems from ordinary differential equations, the map $\tau=\tau_0^1$ is a diffeomorphism (smooth and invertible self-map) of $F$.
$G$-invariant connection
Assume that $\pi:E\to B$ is a bundle with a Lie group $G$ acting freely and transitively on the fibers (and hence on the total space), say, by the right multiplication, $E\times G\to E$, $r:(x,g)\mapsto x\cdot g$, $\pi(x\cdot g)=\pi(x)$. Then is natural to consider the equivariant ($G$-invariant) connections for which the horizontal subspaces $\G_x$ and $\G_{x\cdot g}$ are related by the differential of the corresponding right shift $\rd r(\cdot,g)$.
Such invariance means that for any smooth curve $\gamma$ the corresponding parallel transport $\tau_\gamma:F_0\to F_1$ commutes with the action of $G$: $\tau(x\cdot g)=\tau(x)\cdot g$ for any $g\in G$. In other words, it is sufficient to construct the parallel transport for only one point on the fiber.
Note also that for principal $G$-bundles the tangent spaces $T_x F_b$ to the same fiber $\pi^{-1}(b)$ are canonically isomorphic to each other and to the tangent space $T_e G=\mathfrak g$ which is a Lie algebra of the group $G$. The isomorphism is defined by the differential of the map $(G,e)\to (F,x)$, $g\mapsto x\cdot g$.
Affine connection
If the fiber $F$ of a bundle $\pi:E\to B$ is a (finite-dimensional) vector space, then this linear structure induces the structure of a module (over the ring $C^\infty(B)$ of smooth functions on the base) on the space of sections: for any two sections $s_1,s_2:B\to E$ and any smooth function $f:B\to \R$ the sum $s_1+s_2:B\to E$ and the products $f\cdot s_i:B\to E$ are well-defined smooth sections of $\pi$.
The splitting of the tangent space $T_x E=V_x\oplus \G_x$ into the vertical and horizontal sections defines two commuting linear projections, the horizontal one $T_x E\overset {h_x}\longrightarrow\G_x\overset{\rd \pi}{\longrightarrow} T_{\pi(x)}B$ (parallel to the vertical direction $V_x$) and $v_x:T_x E\to V_x$(parallel to the horizontal direction $\G_x$).
If $s:B\to E$ is a smooth section and $w\in T_b B$ a vector tangent to the base at some point $b\in B$, $\rd s(b)\cdot w\in T_xE$ is a vector tangent to $E$ at $x=s(b)$. The "vertical component" of the this vector, $v_x\cdot \rd s(b)\cdot w\in T_x F_x$ is called the covariant derivative of the section $s$ in direction of $w$. The usual notation is $$ \nabla_w s(b)\in T_{s(b)}F_b. $$ Note that by construction the covariant derivative is linear with respect to $w$, as a composition of linear maps $\rd s(b):T_b B\to T_{s(b)}E$ and $v_x:T_x\to V_x$, $x=s(b)$. If $s_1,s_2$ are two connections, then the corresponding covariant derivative of their sum $s_1+s_2$ is tangent to the same fiber $\pi^{-1}(b)$ yet at the new point $s_1(b)+s_2(b)$, ditto for the section $f\cdot s$.
Definition. The Ehresmann connection on a vector bundle is called affine, if the covariant derivation operator is additive and satisfies the Leibniz rule[2]: $$ \nabla_w (s_1+s_2)(b)=\nabla_w s_1(b)+\nabla_w s_2(b),\qquad \nabla_w (f\cdot s)(b)= (\rd f\cdot w)\cdot s(b)+f(b)\cdot \nabla_w s(b)\qquad\forall b\in B. $$
Covariant derivative in the coordinates
...
- ↑ E.g., if the fiber $F$, is compact, but also if it is a finite-dimensional vector- or $G$-space with $\G'$ linear or $G$-invariant.
- ↑ If we formally declare that $\nabla_w f=\rd f\cdot w\in\R^1$, then the Leibniz formula will take the familiar form $\nabla (f\cdot s)=f\cdot (\nabla s)+(\nabla f)\cdot s$ with respect to the linear structure on $F$
Let  be a smooth locally trivial fibration with typical fibre
be a smooth locally trivial fibration with typical fibre  on which a Lie group
on which a Lie group  acts effectively and smoothly. A connection on this fibre bundle is a mapping of the category of piecewise-smooth curves in the base
acts effectively and smoothly. A connection on this fibre bundle is a mapping of the category of piecewise-smooth curves in the base  into the category of diffeomorphisms of the fibres that associates with a curve
into the category of diffeomorphisms of the fibres that associates with a curve  (with initial point
(with initial point  and end point
and end point  ) a diffeomorphism
) a diffeomorphism  satisfying the following axioms:
satisfying the following axioms:
1) for  ,
,  ,
,  , and
, and 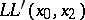 one has
one has
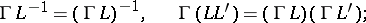 |
2) for an arbitrary trivializing diffeomorphism  and for an
and for an 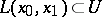 , the diffeomorphism
, the diffeomorphism 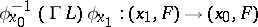 , where
, where 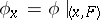 , is defined by the action of some element
, is defined by the action of some element  ;
;
3) for an arbitrary piecewise-smooth parametrization 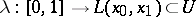 , the mapping
, the mapping  , where
, where 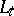 is the image of
is the image of  under
under 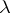 , defines a piecewise-smooth curve in
, defines a piecewise-smooth curve in  that starts from the unit element
that starts from the unit element  ; moreover,
; moreover,  with a common non-zero tangent vector
with a common non-zero tangent vector 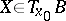 define paths in
define paths in 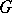 with a common tangent vector
with a common tangent vector 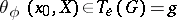 that depends smoothly on
that depends smoothly on 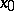 and
and 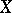 .
.
The diffeomorphism  is called the parallel displacement along
is called the parallel displacement along  . The parallel displacements along all possible closed curves
. The parallel displacements along all possible closed curves  form the holonomy group of the connection
form the holonomy group of the connection 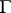 at
at 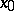 ; this group is isomorphic to a Lie subgroup of
; this group is isomorphic to a Lie subgroup of  that does not depend on
that does not depend on  . A curve
. A curve 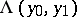 on
on  is said to be horizontal for
is said to be horizontal for 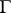 if
if  for any
for any  and some piecewise-smooth parametrization of it. If
and some piecewise-smooth parametrization of it. If 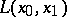 and
and 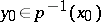 are given, then there always exists a unique horizontal curve
are given, then there always exists a unique horizontal curve 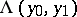 , called the horizontal lift of the curve
, called the horizontal lift of the curve  , such that
, such that  ; it consists of the points
; it consists of the points 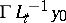 . The set of horizontal lifts of all curves
. The set of horizontal lifts of all curves  in
in  determines the connection
determines the connection 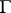 uniquely:
uniquely: 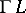 maps the end points of all lifted curves of
maps the end points of all lifted curves of 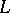 into the initial points.
into the initial points.
A connection is called linear if  depends linearly on
depends linearly on  for any
for any 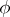 and
and  , or equivalently, if for any
, or equivalently, if for any 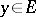 the tangent vectors of the horizontal curves beginning at
the tangent vectors of the horizontal curves beginning at 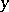 form a vector subspace
form a vector subspace  of
of  , called the horizontal subspace. Here
, called the horizontal subspace. Here  , where
, where  is the fibre through
is the fibre through 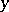 , that is,
, that is, 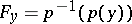 . The smooth distribution
. The smooth distribution  is called the horizontal distribution of the linear connection
is called the horizontal distribution of the linear connection  . It determines
. It determines  uniquely: its integral curves are the horizontal lifts.
uniquely: its integral curves are the horizontal lifts.
A fibre bundle 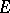 is called principal (respectively, a space of homogeneous type), and is denoted by
is called principal (respectively, a space of homogeneous type), and is denoted by 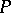 (respectively,
(respectively,  ), if
), if 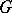 acts simply transitively (respectively, transitively) on
acts simply transitively (respectively, transitively) on  , that is, if for any
, that is, if for any  there is exactly one (respectively, there is an) element
there is exactly one (respectively, there is an) element 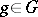 that sends
that sends  to
to  . Suppose that
. Suppose that  acts on
acts on 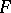 from the left; then a natural action from the right is defined on
from the left; then a natural action from the right is defined on 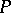 , where
, where  defines
defines  . Here
. Here  is identified with the quotient manifold
is identified with the quotient manifold  formed by the orbits
formed by the orbits 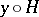 , where
, where  is the stationary subgroup of a point from
is the stationary subgroup of a point from 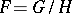 . More generally,
. More generally, 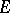 can be identified with the quotient manifold
can be identified with the quotient manifold  of orbits
of orbits 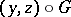 relative to the action defined by
relative to the action defined by 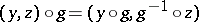 .
.
A smooth distribution  on
on  is a horizontal distribution of some linear connection (which it determines uniquely) if and only if
is a horizontal distribution of some linear connection (which it determines uniquely) if and only if
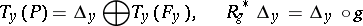 |
for arbitrary 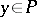 and
and  . All horizontal distributions on
. All horizontal distributions on  (respectively,
(respectively, 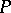 ) are the images of such
) are the images of such  under the canonical projection
under the canonical projection  (respectively, the natural lifts of such
(respectively, the natural lifts of such 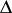 to
to  under the canonical projection
under the canonical projection 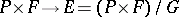 ). Often a linear connection is defined directly as a distribution with the properties mentioned above. It is known that on each
). Often a linear connection is defined directly as a distribution with the properties mentioned above. It is known that on each 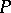 , and so on every
, and so on every 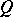 and
and  , there is a linear connection.
, there is a linear connection.
A linear connection in  is usually studied by using its connection form, which determines it uniquely and can be the basis for another definition. An important characteristic of a linear connection is the curvature form; this can be used to compute the Lie algebra of the holonomy group.
is usually studied by using its connection form, which determines it uniquely and can be the basis for another definition. An important characteristic of a linear connection is the curvature form; this can be used to compute the Lie algebra of the holonomy group.
The idea of a connection first arose in 1917 in the work of T. Levi-Civita [1] on parallel displacement of a vector in Riemannian geometry. The notion of an affine connection was introduced by H. Weyl in 1918. In the 1920s E. Cartan (see [3]–[5]) investigated projective and conformal connections (cf. Projective connection; Conformal connection). In 1926 he gave the general concept of a "non-holonomic space with a fundamental group" (see Connections on a manifold), and identified these spaces from the point of view of the general theory of connections. In the 1940s V.V. Vagner developed an even more general concept that is close in spirit (but not in terms of the method) to the modern idea of a connection. 1950 was a decisive year; in it there appeared the survey by Vagner [6], the first notes of G.F. Laptev, which disclosed new approaches, especially analytic ones, and the work of C. Ehresmann [7] that laid the foundation of the modern global theory of connections. See also Weyl connection; Linear connection; Riemannian connection; Symplectic connection; Hermitian connection.
References
| [1] | T. Levi-Civita, "Nozione di parallelismo in una varietà qualunque e consequente specificazione geometrica della curvatura Riemanniana" Rend. Cir. Mat. Palermo , 42 (1917) pp. 173–205 |
| [2] | H. Weyl, "Raum, Zeit, Materie" , Springer (1923) |
| [3] | E. Cartan, "Les espaces à connexion conforme" Ann. Soc. Polon. Math. , 2 (1924) pp. 171–221 |
| [4] | E. Cartan, "Sur les variétés à connexion projective" Bull. Soc. Math. France , 52 (1924) pp. 205–241 |
| [5] | E. Cartan, "Les groupes d'holonomie des espaces généralisés" Acta Math. , 48 (1926) pp. 1–42 |
| [6] | V.V. Vagner, "Theory of a composite manifold" Trudy Sem. Vektor i Tenzor Anal. , 8 (1950) pp. 11–72 (In Russian) |
| [7] | Ch. Ehresmann, "Les connexions infinitésimal dans une espace fibré différentiable" , Colloq. de Topologie Bruxelles, 1950 , G. Thone & Masson (1951) pp. 29–55 |
| [8] | G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential-geometric investigations" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 275–382 (In Russian) |
| [9] | K. Nomizu, "Lie groups and differential geometry" , Math. Soc. Japan (1956) |
| [10] | A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1955) (Translated from French) |
| [11] | Ü.G. Lumiste, "Connection theory in bundle spaces" J. Soviet Math. , 1 (1973) pp. 363–390 Itogi Nauk. Ser. Algebra. Topol. Geom. 1969 , 21 (1971) pp. 123–168 |
Comments
Consider a smooth locally trivial fibre bundle  . A smooth section is a smooth mapping
. A smooth section is a smooth mapping  such that
such that  . This concept generalizes that of a function
. This concept generalizes that of a function 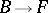 (where
(where 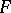 is the fibre of
is the fibre of  ), which is the same as a section of the trivial fibre bundle
), which is the same as a section of the trivial fibre bundle  . In several areas of mathematics it is important to consider sections instead of just functions. E.g. in gauge field theory. But then one would also like to have something like the partial derivatives of a section available, i.e. the quantity that describes to first order how
. In several areas of mathematics it is important to consider sections instead of just functions. E.g. in gauge field theory. But then one would also like to have something like the partial derivatives of a section available, i.e. the quantity that describes to first order how  changes as
changes as  varies (infinitesimally). This requires comparing the fibres of
varies (infinitesimally). This requires comparing the fibres of 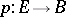 at neighbouring points, but there is nothing in the concept of a fibre bundle as it stands that allows one to do this. For this some extra structure is needed, and that is provided by the idea of a connection.
at neighbouring points, but there is nothing in the concept of a fibre bundle as it stands that allows one to do this. For this some extra structure is needed, and that is provided by the idea of a connection.
It would be simplest if for every two points  one could prescribe an isomorphism
one could prescribe an isomorphism 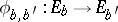 in a consistent way, i.e. such that
in a consistent way, i.e. such that 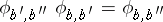 for all triples
for all triples  . Here
. Here  , the fibre of
, the fibre of  over
over 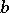 , is of course
, is of course 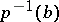 . This, however, would make the bundle trivial, and this is in general not possible. The next best thing would be to have for every smooth path
. This, however, would make the bundle trivial, and this is in general not possible. The next best thing would be to have for every smooth path 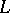 from
from 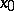 to
to  an isomorphism
an isomorphism 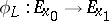 (which may depend on the path
(which may depend on the path 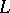 ) from the fibre at the initial point of the path to the fibre at the final point, subject to certain natural restrictions. This is precisely what a connection is.
) from the fibre at the initial point of the path to the fibre at the final point, subject to certain natural restrictions. This is precisely what a connection is.
There are — at least — three intuitively natural ways of describing a connection.
i) Provide for every smooth path  from
from 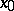 to
to 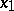 an isomorphism
an isomorphism 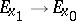 subject to the three conditions 1), 2), 3).
subject to the three conditions 1), 2), 3).
ii) For each  let
let  be the kernel of the tangent mapping at
be the kernel of the tangent mapping at  . The subspace
. The subspace 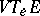 of the tangent space
of the tangent space  to
to  at
at  is called the vertical tangent subspace to
is called the vertical tangent subspace to 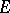 at
at  . Now for each
. Now for each 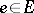 define a complementary subspace
define a complementary subspace 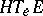 at
at  , called the horizontal tangent subspace at
, called the horizontal tangent subspace at 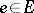 . Thus,
. Thus, 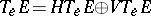 and
and 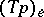 induces an isomorphism
induces an isomorphism  . The
. The 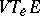 are required to vary smoothly with
are required to vary smoothly with  . In the case of linear connections, cf. above, this is the infinitesimal version of i).
. In the case of linear connections, cf. above, this is the infinitesimal version of i).
iii) Let  be a vector bundle. Then a linear connection can also be specified by giving so to speak the partial derivatives of a section directly (covariant differentiation). This leads to the specification of a bilinear mapping
be a vector bundle. Then a linear connection can also be specified by giving so to speak the partial derivatives of a section directly (covariant differentiation). This leads to the specification of a bilinear mapping  , where
, where  is the space of vector fields on
is the space of vector fields on 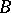 and
and 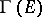 is the space of sections of
is the space of sections of 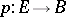 , with certain properties; cf. Linear connection for these properties in the case
, with certain properties; cf. Linear connection for these properties in the case 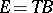 . One consequence of these properties is that
. One consequence of these properties is that  ,
, 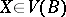 ,
, 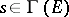 , depends only on
, depends only on  at
at 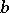 . If
. If  is a smooth path starting in
is a smooth path starting in  with tangent vector
with tangent vector 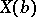 at
at  , then
, then
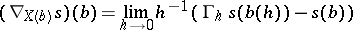 |
where  is parallel displacement defined by
is parallel displacement defined by  .
.
An elegant and convenient way to describe a linear connection in the case that  is a vector bundle is as follows. Let
is a vector bundle is as follows. Let
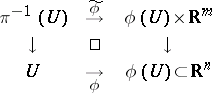 |
be a local chart of  and a trivialization of
and a trivialization of 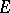 . Then above
. Then above  one has the following local trivialization of
one has the following local trivialization of 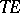 :
:
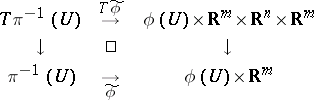 |
where the right-hand arrow is projection in the first two factors. A linear connection on  is now given by a bundle mapping
is now given by a bundle mapping 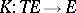 (i.e. the diagram
(i.e. the diagram
 |
is commutative, and  is linear in the fibres), such that locally the mapping looks like
is linear in the fibres), such that locally the mapping looks like
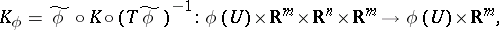 |
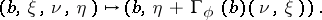 |
The 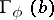 are the Christoffel symbols (relative to the trivialization
are the Christoffel symbols (relative to the trivialization  ; in case
; in case  ,
, 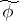 can be taken equal to
can be taken equal to  so that the Christoffel symbols depend only on the chart
so that the Christoffel symbols depend only on the chart 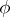 ).
).
Given the connection 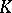 , the horizontal subspace
, the horizontal subspace  is defined by
is defined by
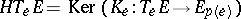 |
and the covariant derivative of a section 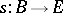 along a vector field
along a vector field  is the section
is the section 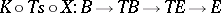 .
.
In the case of infinite-dimensional manifolds and bundles this last notion of a linear connection appears to be the appropriate replacement of the more traditional covariant derivative 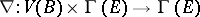 , cf. [a2], Sect. 1.1.
, cf. [a2], Sect. 1.1.
References
| [a1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) pp. Chapt. 4 |
| [a2] | W. Klingenberg, "Lectures on closed geodesics" , Springer (1979) |
Yakovenko/sandbox1. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Yakovenko/sandbox1&oldid=26704