Intersection theory
on an algebraic variety
The theory of intersections of algebraic subvarieties and cycles. Let 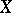 be a smooth algebraic variety of dimension
be a smooth algebraic variety of dimension  over a field
over a field  , while
, while  and
and 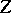 are subvarieties of
are subvarieties of  of codimension
of codimension 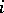 and
and  , respectively. If
, respectively. If  and
and  intersect transversally, then
intersect transversally, then 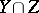 is a smooth subvariety of codimension
is a smooth subvariety of codimension 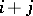 , which is denoted by
, which is denoted by 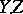 . In the general case, the pair
. In the general case, the pair 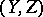 constitutes an algebraic cycle
constitutes an algebraic cycle 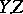 of codimension
of codimension 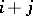 . The idea behind this definition is that
. The idea behind this definition is that 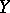 and
and 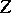 are replaced by cycles
are replaced by cycles 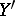 and
and 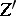 that are equivalent in some sense but that are in general position, and one then takes the intersection of
that are equivalent in some sense but that are in general position, and one then takes the intersection of 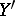 and
and 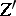 ; of course, the cycle
; of course, the cycle 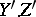 is also defined up to equivalence.
is also defined up to equivalence.
Let 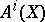 be the group of classes of algebraic cycles of codimension
be the group of classes of algebraic cycles of codimension 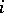 on
on  modulo rational equivalence; let
modulo rational equivalence; let 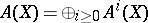 . Chow's intersection theory consists of the construction:
. Chow's intersection theory consists of the construction:
a) of a graded commutative ring structure on 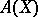 for each smooth quasi-projective variety
for each smooth quasi-projective variety 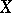 ;
;
b) of a homomorphism of graded rings 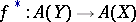 for each morphism
for each morphism 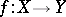 (inverse image); and
(inverse image); and
c) of a homomorphism of groups  of degree
of degree 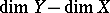 for each proper morphism
for each proper morphism 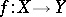 (direct image).
(direct image).
Between the constructions a), b), c) there are a number of relations, of which the main ones are as follows:
the projection formula: For a proper morphism 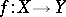 and cycles
and cycles 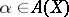 and
and 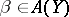 ,
,
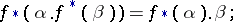 |
reduction to the diagonal: If 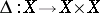 is the diagonal morphism, and
is the diagonal morphism, and 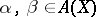 , then
, then 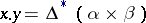 .
.
Also, there exists a natural homomorphism
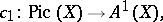 |
which enables one to construct the theory of Chern classes (cf. Chern class) with values in Chow rings, and in particular the Chern character
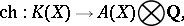 |
which is a ring homomorphism.
It is simplest to determine the direct image homomorphism 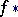 . Let
. Let 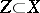 be an irreducible subvariety; if
be an irreducible subvariety; if  , then
, then 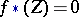 , while if
, while if 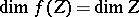 , then
, then 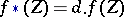 , where
, where 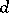 is the degree of
is the degree of 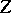 over
over 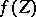 . By linearity, the definition is extended to cycles and classes of cycles. The inverse image homomorphism
. By linearity, the definition is extended to cycles and classes of cycles. The inverse image homomorphism 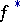 amounts to multiplication of cycles in accordance with
amounts to multiplication of cycles in accordance with
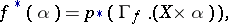 |
where 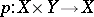 is the projection and
is the projection and 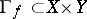 is the graph of
is the graph of  . The definition of multiplication of cycles is given in two stages. Let, initially,
. The definition of multiplication of cycles is given in two stages. Let, initially, 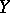 and
and 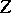 be irreducible subvarieties in
be irreducible subvarieties in 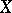 that intersect properly (i.e. the codimension of
that intersect properly (i.e. the codimension of 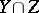 is equal to the sum of the codimensions of
is equal to the sum of the codimensions of 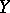 and
and 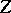 ). Each component
). Each component 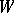 of the intersection
of the intersection 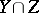 is ascribed some positive integer
is ascribed some positive integer 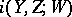 , which is the local multiplicity of the intersection. There are several definitions of
, which is the local multiplicity of the intersection. There are several definitions of 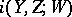 , for example, Serre's Tor-formula:
, for example, Serre's Tor-formula:
 |
where 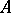 is the local ring
is the local ring  ,
,  and
and 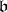 are ideals of
are ideals of 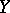 and
and 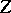 , and
, and 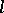 is the length of the
is the length of the 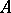 -module. After this, one puts
-module. After this, one puts
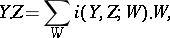 |
where 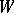 runs through the irreducible components of
runs through the irreducible components of 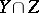 .
.
The second stage is Chow's moving lemma: For any 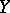 and
and 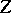 on a quasi-projective variety
on a quasi-projective variety 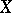 there exists a cycle
there exists a cycle 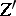 that is rationally equivalent to
that is rationally equivalent to 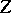 and that intersects properly with
and that intersects properly with 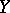 ; moreover, the rational equivalence class of
; moreover, the rational equivalence class of 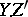 is independent of
is independent of 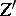 .
.
The most interesting case is that of a projective variety 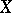 ; applying the direct image functor to the structure morphism
; applying the direct image functor to the structure morphism  one obtains the mapping
one obtains the mapping 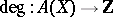 . In essence, the degree of a cycle is the number of points in its zero-dimensional component. The composition of multiplication with the degree enables one to measure an intersection numerically. For example, if
. In essence, the degree of a cycle is the number of points in its zero-dimensional component. The composition of multiplication with the degree enables one to measure an intersection numerically. For example, if 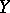 and
and 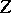 have complementary dimensions, then one obtains the intersection index (in algebraic geometry) (the intersection number) of
have complementary dimensions, then one obtains the intersection index (in algebraic geometry) (the intersection number) of 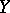 and
and 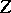 . Similarly, one obtains an intersection index for
. Similarly, one obtains an intersection index for  divisors
divisors 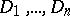 :
:
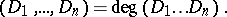 |
For example, the Chow ring for the projective space 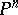 is generated by the class of a hyperplane
is generated by the class of a hyperplane 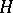 , where
, where 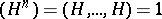 . Therefore, if
. Therefore, if 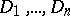 are hypersurfaces of degrees
are hypersurfaces of degrees 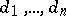 , then
, then 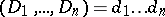 (Bezout's theorem). The degree of a projective variety
(Bezout's theorem). The degree of a projective variety 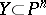 of dimension
of dimension 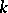 is defined as the intersection index of
is defined as the intersection index of 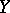 with a linear subspace
with a linear subspace 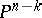 of complementary dimension; if the varieties
of complementary dimension; if the varieties 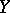 and
and 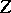 intersect transversally, then the degree of
intersect transversally, then the degree of 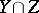 is the product of the degrees of
is the product of the degrees of 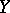 and
and 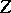 .
.
For properly-intersecting effective divisors 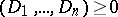 , but in the general case this is not true. For example, for an exceptional curve (cf. Exceptional subvariety)
, but in the general case this is not true. For example, for an exceptional curve (cf. Exceptional subvariety) 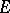 on a surface,
on a surface, 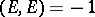 .
.
Other theories have many of the formal properties of the theory of Chow rings: cycles modulo algebraic or numerical equivalence, 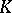 -theory, singular cohomology theory
-theory, singular cohomology theory 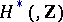 (in the case
(in the case 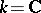 ), and
), and 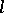 -adic cohomology theory (see also Weil cohomology). This leads to the axiomatic construction of intersection theory by putting each variety
-adic cohomology theory (see also Weil cohomology). This leads to the axiomatic construction of intersection theory by putting each variety 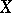 (from some category) into correspondence with a ring
(from some category) into correspondence with a ring 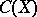 and homomorphisms
and homomorphisms 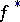 and
and 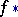 related by axioms of the type of projection or reduction-to-the-diagonal formulas (see [1]). The comparison of different intersection theories leads to useful results. For example, in the complex case, the concept of a fundamental cycle enables one to define an intersection-theory homomorphism
related by axioms of the type of projection or reduction-to-the-diagonal formulas (see [1]). The comparison of different intersection theories leads to useful results. For example, in the complex case, the concept of a fundamental cycle enables one to define an intersection-theory homomorphism 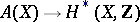 , which enables one to use transcendental methods. Comparison of
, which enables one to use transcendental methods. Comparison of 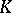 -theory with Chow's theory leads to the Riemann–Roch–Grothendieck theorem (cf. Riemann–Roch theorem). An important part is played here by the intersection theory for monoidal transformations [2], [6]. Another application of intersection theory is related to the foundations of Schubert's geometric calculus [3]. This branch of geometry can be regarded as the theory of Chow rings for various varieties that classify geometric objects: Grassmann manifolds, flag manifolds, etc.
-theory with Chow's theory leads to the Riemann–Roch–Grothendieck theorem (cf. Riemann–Roch theorem). An important part is played here by the intersection theory for monoidal transformations [2], [6]. Another application of intersection theory is related to the foundations of Schubert's geometric calculus [3]. This branch of geometry can be regarded as the theory of Chow rings for various varieties that classify geometric objects: Grassmann manifolds, flag manifolds, etc.
References
| [1] | , Anneaux de Chow et applications , Sem. Chevalley (1958) |
| [2] | Yu.I. Manin, "Lectures on algebraic geometry" , 1 , Moscow (1970) (In Russian) |
| [3] | "Hilbert's problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German) |
| [4] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [5] | J.-P. Serre, "Algèbre locale. Multiplicités" , Lect. notes in math. , 11 , Springer (1965) |
| [6] | P. Berthelot (ed.) A. Grothendieck (ed.) L. Illusie (ed.) et al. (ed.) , Théorie des intersections et théorème de Riemann–Roch (SGA 6) , Lect. notes in math. , 225 , Springer (1971) |
| [7] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [8] | R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1982) |
| [9] | W. Fulton, "Intersection theory" , Springer (1984) |
Comments
W. Fulton has defined Chow groups for singular varieties [a1]. A more refined intersection theory has been developed by Fulton and R. MacPherson: given cycles 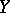 and
and 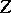 on
on 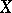 , it gives a well-defined element
, it gives a well-defined element 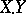 of
of 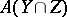 [a2].
[a2].
A new development is the intersection theory for arithmetic varieties, i.e. flat schemes over the ring of integers of number fields with suitable extra data for the infinite places, [a3]–.
References
| [a1] | W. Fulton, "Rational equivalence on singular varieties" Publ. Math. IHES , 45 (1975) pp. 147–167 |
| [a2] | W. Fulton, R.D. MacPherson, "Defining algebraic intersections" L.D. Olson (ed.) , Algebraic geometry , Lect. notes in math. , 687 , Springer (1978) pp. 1–30 |
| [a3] | G. Faltings, "Calculus on arithmetic surfaces" Ann. of Math. , 119 (1984) pp. 387–424 |
| [a4] | S. Arakelov, "Intersection theory of divisors on an arithmetical surface" Math. USSR Izv. , 8 (1974) pp. 1167–1180 Izv. Akad. Nauk. SSSR Ser. Mat. , 38 : 6 (1974) pp. 1179–1192 |
| [a5] | H. Gillet, "An introduction to higher dimensional Arakelov theory" K.A. Ribet (ed.) , Current trends in arithmetical algebraic geometry , Contemp. Math. , 67 , Amer. Math. Soc. (1987) pp. 209–228 |
Intersection theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Intersection_theory&oldid=19158