Regularization of sequences
Let 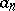 ,
, 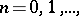 be a sequence of real numbers (indexed by the non-negative integers). A regularization of
be a sequence of real numbers (indexed by the non-negative integers). A regularization of  is a sequence
is a sequence 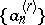 obtained from
obtained from 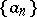 by replacing certain
by replacing certain 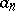 which are "excessively high" with respect to the others by suitable lower values. An important application of regularized sequences is to the problem of equivalence of classes of
which are "excessively high" with respect to the others by suitable lower values. An important application of regularized sequences is to the problem of equivalence of classes of 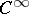 -functions; that is, the problem of when two sequences of constants determine the same quasi-analytic class of functions. The answers tend to be given in the form that the two sequences
-functions; that is, the problem of when two sequences of constants determine the same quasi-analytic class of functions. The answers tend to be given in the form that the two sequences 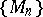 and
and 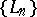 determine the same quasi-analytic class if suitably regularized sequences
determine the same quasi-analytic class if suitably regularized sequences 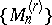 and
and 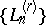 are the same, cf. [a1], [a2].
are the same, cf. [a1], [a2].
Some important regularization procedures are as follows. A sequence 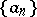 of real numbers is called a convex sequence if the function
of real numbers is called a convex sequence if the function 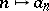 is convex, i.e. if for all
is convex, i.e. if for all 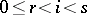 ,
,
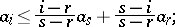 |
that is, if the point  is located below or on the segment in the plane joining
is located below or on the segment in the plane joining 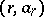 and
and 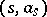 (cf. Convex function (of a real variable)).
(cf. Convex function (of a real variable)).
The convex regularization, or Newton regularization, 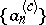 of
of 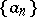 is the largest convex minorant of
is the largest convex minorant of 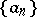 (cf. Majorant and minorant, 1)).
(cf. Majorant and minorant, 1)).
The log-convex regularization, or convex regularization by means of the logarithm, of a sequence of positive numbers 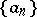 is the sequence of positive numbers
is the sequence of positive numbers 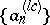 such that
such that 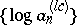 is the convex regularization of
is the convex regularization of 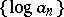 . It is defined by the relations
. It is defined by the relations
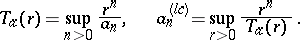 |
The exponential regularization 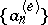 of
of 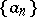 is defined by the relations
is defined by the relations
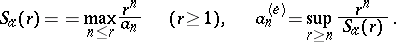 |
The Newton regularization of a sequence 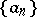 is very much related to the Newton polygon of
is very much related to the Newton polygon of 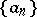 (this explains the name "Newton regularization" , cf. also Newton diagram, which discusses the context in which the Newton polygon first arose). For a finite sequence
(this explains the name "Newton regularization" , cf. also Newton diagram, which discusses the context in which the Newton polygon first arose). For a finite sequence 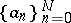 , its Newton polygon is the highest convex polygonal line in
, its Newton polygon is the highest convex polygonal line in 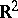 joining
joining 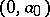 to
to 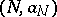 , i.e. it is the polygonal line consisting of the segments joining
, i.e. it is the polygonal line consisting of the segments joining 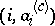 to
to 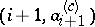 ,
, 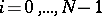 . Thus, the number
. Thus, the number 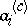 is the ordinate of the point of the Newton polygon of
is the ordinate of the point of the Newton polygon of 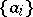 with abscissa
with abscissa 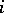 .
.
An example of this for the sequence 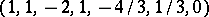 ,
,  , with convex regularization
, with convex regularization 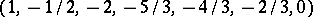 , is given in Fig. a.
, is given in Fig. a.
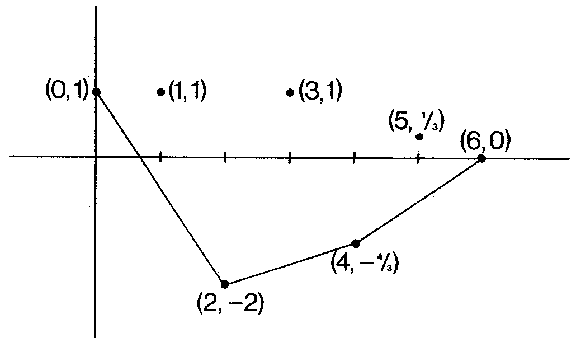
Figure: r080940a
To avoid certain pathologies (like 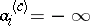 for all
for all 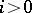 ), let
), let 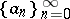 be bounded from below. The Newton polygon of this sequence is defined as the limit of the Newton polygons of the finite sequences
be bounded from below. The Newton polygon of this sequence is defined as the limit of the Newton polygons of the finite sequences 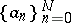 as
as 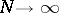 . It remains true that
. It remains true that 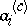 is determined by the condition that
is determined by the condition that 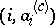 lies on the Newton polygon of
lies on the Newton polygon of 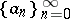 .
.
Let 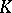 be a non-Archimedean valued field with valuation
be a non-Archimedean valued field with valuation  (cf. also Norm on a field). Let
(cf. also Norm on a field). Let 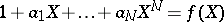 be a polynomial of degree
be a polynomial of degree  over
over 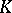 . The Newton polygon of the polynomial
. The Newton polygon of the polynomial 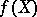 is the Newton polygon of the sequence
is the Newton polygon of the sequence 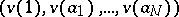 . It carries immediate information on the valuations of the roots of
. It carries immediate information on the valuations of the roots of 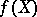 (in a complete algebraic closure of
(in a complete algebraic closure of 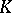 ). Indeed, if
). Indeed, if 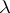 is the slope of a segment of the Newton polygon of (abscissa) length
is the slope of a segment of the Newton polygon of (abscissa) length  , then there are precisely
, then there are precisely  roots of valuation
roots of valuation 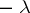 (counted with multiplicities); an analogous result holds for roots of power series (this is related to a
(counted with multiplicities); an analogous result holds for roots of power series (this is related to a 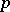 -adic Weierstrass preparation theorem, cf. (the editorial comments to) Weierstrass theorem, and [a3]).
-adic Weierstrass preparation theorem, cf. (the editorial comments to) Weierstrass theorem, and [a3]).
The Newton polygon of a sequence 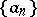 can be obtained geometrically as follows. For all
can be obtained geometrically as follows. For all 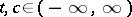 one considers the line
one considers the line 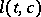 in
in 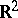 through
through 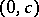 of slope
of slope 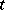 ; it is given by the equation
; it is given by the equation 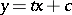 . Let
. Let 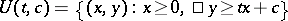 be the supergraph of
be the supergraph of 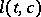 . Let
. Let 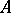 be the graph of
be the graph of 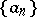 ,
, 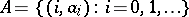 . Then the Newton polygon is the lower boundary of the convex set
. Then the Newton polygon is the lower boundary of the convex set
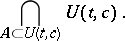 |
As noted, the Newton regularization (convex regularization) of a sequence 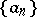 is determined by its Newton polygon. This construction has been generalized. Let
is determined by its Newton polygon. This construction has been generalized. Let 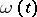 be a non-decreasing function of
be a non-decreasing function of 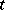 with values in
with values in 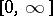 . Let
. Let
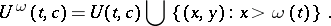 |
The lower boundary of
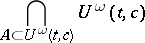 |
now defines the  -regularized sequence
-regularized sequence 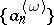 . Newton and exponential regularization correspond to
. Newton and exponential regularization correspond to 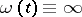 and
and 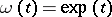 , respectively.
, respectively.
References
| [a1] | S. Mandelbrojt, "Séries adhérentes, régularisations des suites, applications" , Gauthier-Villars (1952) |
| [a2] | J.A. Siddigi, "On the equivalence of classes of infinitely differentiable functions" Soviet J. Contemp. Math. Anal. Arm. Acad. Sci. , 19 : 1 (1984) pp. 18–29 Izv. Akad. Nauk Arm.SSR Mat. , 19 : 1 (1984) pp. 19–30 |
| [a3] | N. Koblitz, "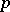 -adic numbers, -adic numbers, 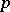 -adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4 -adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4 |
Regularization of sequences. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regularization_of_sequences&oldid=19031