Regular torus

An algebraic torus in a connected algebraic group (over an algebraically closed field) that is contained in only a finite number of Borel subgroups (cf. Borel subgroup). The maximal tori in are always regular (cf. Maximal torus). In general, a torus is regular if and only if its centralizer is a solvable group. One-dimensional regular tori and their corresponding one-parameter subgroups (also called regular) play an important role in algebraic group theory. A torus that is not regular is called singular. For reductive groups (cf. Reductive group), a criterion for the singularity of a torus can be given in terms of root systems. 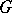Thus, if is a maximal torus in containing 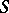and 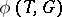is the corresponding root system, then is singular if and only if for some .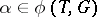

A regular torus in 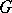is sometimes defined as a torus 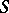that contains a regular element (an element is regular if the dimension of the centralizer 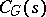in 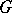is minimal), and it is then called a semi-regular torus if it is regular in the sense of the original definition (see, for example, [1]). Both these definitions are equivalent for reductive groups.

References

[1]	A. Borel, "Linear algebraic groups" , Benjamin (1969)
[2]	J.E. Humphreys, "Linear algebraic groups" , Springer (1975)