Geodesic circle

The set of points on a metric two-dimensional manifold whose distance from a fixed point 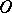is a constant . A special case is a circle in the Euclidean plane.

If is small, a geodesic circle on a regular surface and, in general, in a two-dimensional Riemannian space is a simple closed curve (not necessarily of a constant geodesic curvature); each one of its points may be connected with 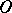by a unique shortest line (the radius or radial geodesic), forming a right angle with the geodesic circle; a geodesic circle bounds a convex region. If 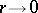, the length 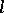of a geodesic circle is connected with the Gaussian curvature 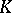at the point 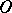by the relation

If is large, more than one radial geodesic may lead to the same point on the geodesic circle, the circle may bound a non-convex region and may consist of several components. A geodesic circle is frequently employed in studies in global geometry. The properties of geodesic circles on general convex surfaces and in manifolds with an irregular metric were studied in [1].

A geodesic circle in the sense of Darboux is a closed curve of constant geodesic curvature. It is a stationary curve for the isoperimetric problem. It coincides with an ordinary geodesic circle on surfaces of constant curvature [2].

References

[1]	Yu.D. Bugaro, M.B. Stratilatova, "Circumferences on a surface" Proc. Steklov Inst. Math. , 76 (1965) pp. 109–141 Trudy Mat. Inst. Steklov. , 76 (1965) pp. 88–114
[2]	W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Affine Differentialgeometrie" , 2 , Springer (1923)

Comments

Both types of geodesic circles are also considered in a more general setting. The first one is generalized to the concept of a distance sphere in a Riemannian manifold. The generalization of the second one appears under the notion of an extrinsic sphere, which is characterized as a totally umbilical submanifold having non-vanishing parallel mean curvature normal [a3].

References

[a1]	K. Nomizu, K. Yano, "On circles and spheres in Riemannian geometry" Math. Ann. , 210 (1974) pp. 163–170
[a2]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)
[a3]	B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973)