Geodesic circle
The set of points on a metric two-dimensional manifold whose distance from a fixed point 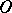 is a constant
is a constant  . A special case is a circle in the Euclidean plane.
. A special case is a circle in the Euclidean plane.
If  is small, a geodesic circle on a regular surface and, in general, in a two-dimensional Riemannian space is a simple closed curve (not necessarily of a constant geodesic curvature); each one of its points may be connected with
is small, a geodesic circle on a regular surface and, in general, in a two-dimensional Riemannian space is a simple closed curve (not necessarily of a constant geodesic curvature); each one of its points may be connected with 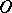 by a unique shortest line (the radius or radial geodesic), forming a right angle with the geodesic circle; a geodesic circle bounds a convex region. If
by a unique shortest line (the radius or radial geodesic), forming a right angle with the geodesic circle; a geodesic circle bounds a convex region. If 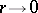 , the length
, the length 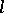 of a geodesic circle is connected with the Gaussian curvature
of a geodesic circle is connected with the Gaussian curvature 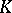 at the point
at the point 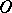 by the relation
by the relation
 |
If  is large, more than one radial geodesic may lead to the same point on the geodesic circle, the circle may bound a non-convex region and may consist of several components. A geodesic circle is frequently employed in studies in global geometry. The properties of geodesic circles on general convex surfaces and in manifolds with an irregular metric were studied in [1].
is large, more than one radial geodesic may lead to the same point on the geodesic circle, the circle may bound a non-convex region and may consist of several components. A geodesic circle is frequently employed in studies in global geometry. The properties of geodesic circles on general convex surfaces and in manifolds with an irregular metric were studied in [1].
A geodesic circle in the sense of Darboux is a closed curve of constant geodesic curvature. It is a stationary curve for the isoperimetric problem. It coincides with an ordinary geodesic circle on surfaces of constant curvature [2].
References
| [1] | Yu.D. Bugaro, M.B. Stratilatova, "Circumferences on a surface" Proc. Steklov Inst. Math. , 76 (1965) pp. 109–141 Trudy Mat. Inst. Steklov. , 76 (1965) pp. 88–114 |
| [2] | W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Affine Differentialgeometrie" , 2 , Springer (1923) |
Comments
Both types of geodesic circles are also considered in a more general setting. The first one is generalized to the concept of a distance sphere in a Riemannian manifold. The generalization of the second one appears under the notion of an extrinsic sphere, which is characterized as a totally umbilical submanifold having non-vanishing parallel mean curvature normal [a3].
References
| [a1] | K. Nomizu, K. Yano, "On circles and spheres in Riemannian geometry" Math. Ann. , 210 (1974) pp. 163–170 |
| [a2] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a3] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
Geodesic circle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_circle&oldid=17403