Weierstrass theorem
Weierstrass' infinite product theorem [1]: For any given sequence of points in the complex plane 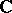 ,
,
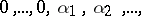 | (1) |
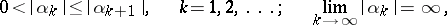 |
there exists an entire function with zeros at the points 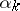 of this sequence and only at these points. This function may be constructed as a canonical product:
of this sequence and only at these points. This function may be constructed as a canonical product:
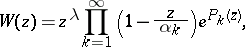 | (2) |
where 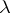 is the multiplicity of zero in the sequence (1), and
is the multiplicity of zero in the sequence (1), and
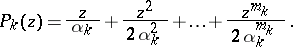 |
The multipliers
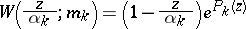 |
are called Weierstrass prime multipliers or elementary factors. The exponents 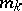 are chosen so as to ensure the convergence of the product (2); for instance, the choice
are chosen so as to ensure the convergence of the product (2); for instance, the choice 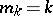 ensures the convergence of (2) for any sequence of the form (1).
ensures the convergence of (2) for any sequence of the form (1).
It also follows from this theorem that any entire function 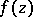 with zeros (1) has the form
with zeros (1) has the form
 |
where 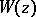 is the canonical product (2) and
is the canonical product (2) and 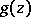 is an entire function (see also Hadamard theorem on entire functions).
is an entire function (see also Hadamard theorem on entire functions).
Weierstrass' infinite product theorem can be generalized to the case of an arbitrary domain 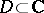 : Whatever a sequence of points
: Whatever a sequence of points 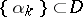 without limit points in
without limit points in 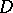 , there exists a holomorphic function
, there exists a holomorphic function 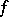 in
in 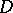 with zeros at the points
with zeros at the points 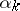 and only at these points.
and only at these points.
The part of the theorem concerning the existence of an entire function with arbitrarily specified zeros may be generalized to functions of several complex variables as follows: Let each point 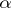 of the complex space
of the complex space 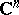 ,
, 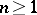 , be brought into correspondence with one of its neighbourhoods
, be brought into correspondence with one of its neighbourhoods 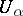 and with a function
and with a function 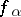 which is holomorphic in
which is holomorphic in  . Moreover, suppose this is done in such a way that if the intersection
. Moreover, suppose this is done in such a way that if the intersection 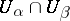 of the neighbourhoods of the points
of the neighbourhoods of the points 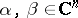 is non-empty, then the fraction
is non-empty, then the fraction 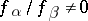 is a holomorphic function in
is a holomorphic function in 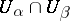 . Under these conditions there exists an entire function
. Under these conditions there exists an entire function 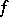 in
in 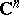 such that the fraction
such that the fraction 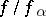 is a holomorphic function at every point
is a holomorphic function at every point 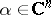 . This theorem is known as Cousin's second theorem (see also Cousin problems).
. This theorem is known as Cousin's second theorem (see also Cousin problems).
References
| [1] | K. Weierstrass, "Math. Werke" , 1–7 , Mayer & Müller (1894–1895) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) |
Comments
References
| [a1] | R. Remmert, "Funktionentheorie" , II , Springer (1991) |
Weierstrass' theorem on the approximation of functions: For any continuous real-valued function 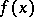 on the interval
on the interval 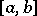 there exists a sequence of algebraic polynomials
there exists a sequence of algebraic polynomials 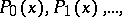 which converges uniformly on
which converges uniformly on 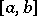 to the function
to the function 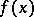 ; established by K. Weierstrass .
; established by K. Weierstrass .
Similar results are valid for all spaces 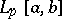 . The Jackson theorem is a strengthening of this theorem.
. The Jackson theorem is a strengthening of this theorem.
The theorem is also valid for real-valued continuous 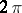 -periodic functions and trigonometric polynomials, e.g. for real-valued functions which are continuous on a bounded closed domain in an
-periodic functions and trigonometric polynomials, e.g. for real-valued functions which are continuous on a bounded closed domain in an 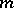 -dimensional space, or for polynomials in
-dimensional space, or for polynomials in 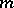 variables. For generalizations, see Stone–Weierstrass theorem. For the approximation of functions of a complex variable by polynomials, see [3].
variables. For generalizations, see Stone–Weierstrass theorem. For the approximation of functions of a complex variable by polynomials, see [3].
References
| [1a] | K. Weierstrass, "Über die analytische Darstellbarkeit sogenannter willkülicher Funktionen reeller Argumente" Sitzungsber. Akad. Wiss. Berlin (1885) pp. 633–639; 789–805 |
| [1b] | K. Weierstrass, "Über die analytische Darstellbarkeit sogenannter willkülicher Funktionen reeller Argumente" , Werke , 3 , Preuss. Akad. Wiss. (1903) |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) |
Yu.N. Subbotin
Comments
References
| [a1] | D. Gaier, "Vorlesungen über Approximation im Komplexen" , Birkhäuser (1980) |
| [a2] | J. Wermer, "Banach algebras and several complex variables" , Springer (1976) |
Weierstrass' theorem on uniformly convergent series of analytic functions : If the terms of a series
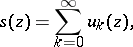 | (*) |
which converges uniformly on compacta inside a domain 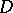 of the complex plane
of the complex plane 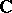 , are analytic functions in
, are analytic functions in 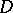 , then the sum
, then the sum 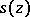 is an analytic function in
is an analytic function in 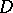 . Moreover, the series
. Moreover, the series
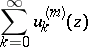 |
obtained by 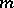 successive term-by-term differentiations of the series (*), for any
successive term-by-term differentiations of the series (*), for any 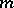 , also converges uniformly on compacta inside
, also converges uniformly on compacta inside 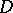 towards the derivative
towards the derivative  of the sum of the series (*). This theorem has been generalized to series of analytic functions of several complex variables converging uniformly on compacta inside a domain
of the sum of the series (*). This theorem has been generalized to series of analytic functions of several complex variables converging uniformly on compacta inside a domain 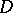 of the complex space
of the complex space 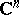 ,
,  , and the series of partial derivatives of a fixed order of the terms of the series (*) converges uniformly to the respective partial derivative of the sum of the series:
, and the series of partial derivatives of a fixed order of the terms of the series (*) converges uniformly to the respective partial derivative of the sum of the series:
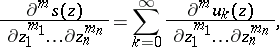 |
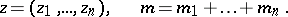 |
Weierstrass' theorem on uniform convergence on the boundary of a domain : If the terms of a series
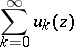 |
are continuous in a closed bounded domain 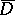 of the complex plane
of the complex plane 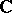 and are analytic in
and are analytic in 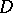 , then uniform convergence of this series on the boundary of the domain implies that it converges uniformly on the closed domain
, then uniform convergence of this series on the boundary of the domain implies that it converges uniformly on the closed domain 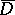 .
.
This property of series of analytic functions is also applicable to analytic and harmonic functions defined, respectively, in a domain of the complex space  ,
, 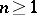 , or in the Euclidean space
, or in the Euclidean space 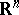 ,
, 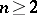 . As a general rule it remains valid in all situations in which the maximum-modulus principle is applicable.
. As a general rule it remains valid in all situations in which the maximum-modulus principle is applicable.
References
| [1a] | K. Weierstrass, "Abhandlungen aus der Funktionenlehre" , Springer (1866) |
| [1b] | K. Weierstrass, "Math. Werke" , 1–7 , Mayer & Müller (1894–1895) |
| [2] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , 1 , Cambridge Univ. Press (1952) pp. Chapt. 3 |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) pp. Chapts. 3; 7 (Translated from Russian) |
Comments
References
| [a1] | R. Remmert, "Theory of complex functions" , 1 , Springer (1990) (Translated from German) |
Weierstrass' preparation theorem. A theorem obtained and originally formulated by K. Weierstrass
in 1860 as a preparation lemma, used in the proofs of the existence and analytic nature of the implicit function of a complex variable defined by an equation 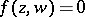 whose left-hand side is a holomorphic function of two complex variables. This theorem generalizes the following important property of holomorphic functions of one complex variable to functions of several complex variables: If
whose left-hand side is a holomorphic function of two complex variables. This theorem generalizes the following important property of holomorphic functions of one complex variable to functions of several complex variables: If 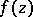 is a holomorphic function of
is a holomorphic function of  in a neighbourhood of the coordinate origin with
in a neighbourhood of the coordinate origin with 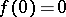 ,
, 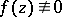 , then it may be represented in the form
, then it may be represented in the form 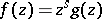 , where
, where  is the multiplicity of vanishing of
is the multiplicity of vanishing of 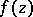 at the coordinate origin,
at the coordinate origin, 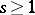 , while the holomorphic function
, while the holomorphic function 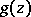 is non-zero in a certain neighbourhood of the origin.
is non-zero in a certain neighbourhood of the origin.
The formulation of the Weierstrass preparation theorem for functions of  complex variables,
complex variables, 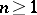 . Let
. Let
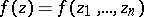 |
be a holomorphic function of 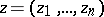 in the polydisc
in the polydisc
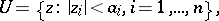 |
and let
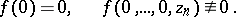 |
Then, in some polydisc
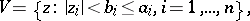 |
the function 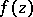 can be represented in the form
can be represented in the form
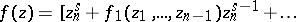 |
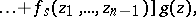 |
where  is the multiplicity of vanishing of the function
is the multiplicity of vanishing of the function
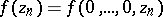 |
at the coordinate origin, 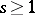 ; the functions
; the functions 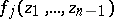 are holomorphic in the polydisc
are holomorphic in the polydisc
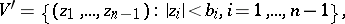 |
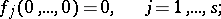 |
the function 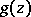 is holomorphic and does not vanish in
is holomorphic and does not vanish in 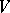 . The functions
. The functions 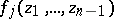 ,
, 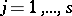 , and
, and 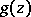 are uniquely determined by the conditions of the theorem.
are uniquely determined by the conditions of the theorem.
If the formulation is suitably modified, the coordinate origin may be replaced by any point  of the complex space
of the complex space 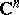 . It follows from the Weierstrass preparation theorem that for
. It follows from the Weierstrass preparation theorem that for  , as distinct from the case of one complex variable, every neighbourhood of a zero of a holomorphic function contains an infinite set of other zeros of this function.
, as distinct from the case of one complex variable, every neighbourhood of a zero of a holomorphic function contains an infinite set of other zeros of this function.
Weierstrass' preparation theorem is purely algebraic, and may be formulated for formal power series. Let 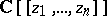 be the ring of formal power series in the variables
be the ring of formal power series in the variables  with coefficients in the field of complex numbers
with coefficients in the field of complex numbers  ; let
; let  be a series of this ring whose terms have lowest possible degree
be a series of this ring whose terms have lowest possible degree 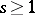 , and assume that a term of the form
, and assume that a term of the form 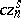 ,
, 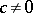 , exists. The series
, exists. The series 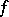 can then be represented as
can then be represented as
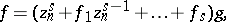 |
where 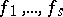 are series in
are series in 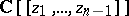 whose constant terms are zero, and
whose constant terms are zero, and 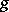 is a series in
is a series in  with non-zero constant term. The formal power series
with non-zero constant term. The formal power series 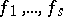 and
and 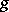 are uniquely determined by
are uniquely determined by 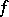 .
.
A meaning which is sometimes given to the theorem is the following division theorem: Let the series
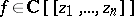 |
satisfy the conditions just specified, and let 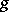 be an arbitrary series in
be an arbitrary series in 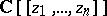 . Then there exists a series
. Then there exists a series
 |
and series
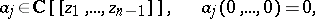 |
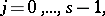 |
which satisfy the following equation:
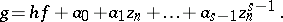 |
Weierstrass' preparation theorem also applies to rings of formally bounded series. It provides a method of inductive transition, e.g. from 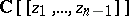 to
to 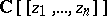 . It is possible to establish certain properties of the rings
. It is possible to establish certain properties of the rings 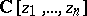 and
and  in this way, such as being Noetherian and having the unique factorization property. There exists a generalization of this theorem to differentiable functions [6].
in this way, such as being Noetherian and having the unique factorization property. There exists a generalization of this theorem to differentiable functions [6].
References
| [1a] | K. Weierstrass, "Abhandlungen aus der Funktionenlehre" , Springer (1866) |
| [1b] | K. Weierstrass, "Math. Werke" , 1–7 , Mayer & Müller (1894–1895) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) |
| [3] | S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948) |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [5] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [6] | B. Malgrange, "Ideals of differentiable functions" , Tata Inst. (1966) |
Comments
The polynomial
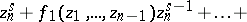 |
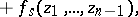 |
which occurs in the Weierstrass preparation theorem, is called a Weierstrass polynomial of degree  in
in 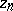 .
.
The analogue of the Weierstrass preparation theorem for differentiable functions is variously known as the differentiable preparation theorem, the Malgrange preparation theorem or the Malgrange–Mather preparation theorem. Let 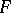 be a smooth real-valued function on some neighbourhood of
be a smooth real-valued function on some neighbourhood of  in
in 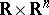 and let
and let 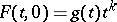 with
with 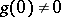 and
and 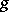 smooth near
smooth near  in
in 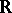 . Then the Malgrange preparation theorem says that there exists a smooth function
. Then the Malgrange preparation theorem says that there exists a smooth function  near zero such that
near zero such that  for suitable smooth
for suitable smooth 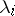 , and the Mather division theorem says that for any smooth
, and the Mather division theorem says that for any smooth 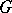 near
near  in
in  there exist smooth functions
there exist smooth functions 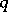 and
and  on
on  near
near  such that
such that 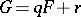 with
with 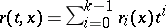 . For more sophisticated versions of the differentiable preparation and division theorems, cf. [a2]–[a4].
. For more sophisticated versions of the differentiable preparation and division theorems, cf. [a2]–[a4].
An important application is the differentiable symmetric function theorem (differentiable Newton theorem), which says that a germ 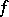 of a symmetric differentiable function of
of a symmetric differentiable function of  in
in  can be written as a germ of a differentiable function in the elementary symmetric functions
can be written as a germ of a differentiable function in the elementary symmetric functions 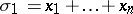 ,
, 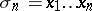 , [a7], [a8].
, [a7], [a8].
There exist also 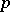 -adic analogues of the preparation and division theorems. Let
-adic analogues of the preparation and division theorems. Let 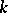 be a complete non-Archimedean normed field (cf. Norm on a field).
be a complete non-Archimedean normed field (cf. Norm on a field). 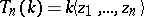 is the algebra of power series
is the algebra of power series 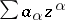 ,
, 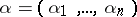 ,
,  ,
, 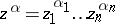 , such that
, such that 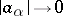 as
as 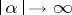 ,
, 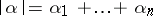 . The norm on
. The norm on 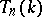 is defined by
is defined by 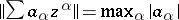 . The subring
. The subring 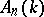 consists of all
consists of all 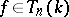 with
with 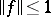 and
and 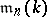 is the ideal of all
is the ideal of all 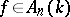 with
with 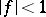 . Let
. Let  be the residue ring
be the residue ring 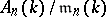 , and let
, and let 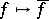 be the quotient mapping. Then
be the quotient mapping. Then 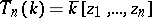 , where
, where 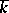 is the residue field of
is the residue field of 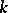 . An element
. An element 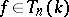 with
with 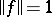 is called regular in
is called regular in 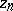 of degree
of degree 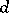 if
if 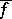 is of the form
is of the form 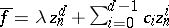 with
with 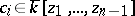 and
and 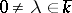 . Note that
. Note that 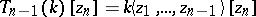 is naturally a subalgebra of
is naturally a subalgebra of 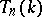 . The
. The 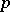 -adic Weierstrass preparation and division theorem now says: i) (division) Let
-adic Weierstrass preparation and division theorem now says: i) (division) Let 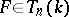 be regular of degree
be regular of degree 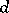 in
in 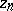 and let
and let 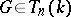 . Then there exist unique elements
. Then there exist unique elements 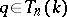 and
and 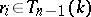 ,
, 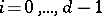 , such that
, such that 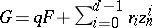 and, moreover,
and, moreover, 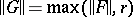 , where
, where 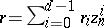 ; ii) (preparation) Let
; ii) (preparation) Let 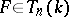 be of norm
be of norm 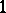 , then there exists a
, then there exists a 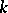 -automorphism of
-automorphism of 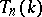 such that
such that 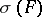 is regular in
is regular in  .
.
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4 |
| [a2] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) pp. Chapt. IV |
| [a3] | J.C. Tougeron, "Ideaux de fonction différentiables" , Springer (1972) pp. Chapt. IX |
| [a4] | B. Malgrange, "Ideals of differentiable functions" , Oxford Univ. Press (1966) pp. Chapt. V |
| [a5] | J. Fresnel, M. van der Put, "Géométrie analytique rigide et applications" , Birkhäuser (1981) pp. §II.2 |
| [a6] | N. Koblitz, "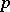 -adic numbers, -adic numbers, 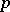 -adic analysis, and zeta-functions" , Springer (1977) pp. 97 -adic analysis, and zeta-functions" , Springer (1977) pp. 97 |
| [a7] | G. Glaeser, "Fonctions composés différentiables" Ann. of Math. , 77 (1963) pp. 193–209 |
| [a8] | S. Łojasiewicz, "Whitney fields and the Malgrange–Mather preparation theorem" C.T.C. Wall (ed.) , Proc. Liverpool Singularities Symposium I , Lect. notes in math. , 192 , Springer (1971) pp. 106–115 |
Weierstrass theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_theorem&oldid=16899