Prime ring

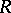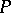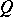A ring in which the product of two two-sided ideals (cf. Ideal) and is equal to the zero ideal if and only if eithe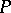r or 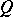is the zero ideal. In other words, the ideals of a prime ring form a semi-group without zero divisors under multiplication. A ring 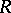is a prime ring if and only if the right (left) annihilator of any non-zero right (correspondingly, left) ideal of it is equal to , and also if and only if 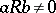for any non-zero 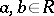. The centre of a prime ring is an integral domain. Any primitive ring is prime. If a ring 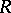does not contain non-zero nil ideals, then 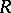is the subdirect sum of prime rings. The class of prime rings plays an important part in the theory of radicals of rings (cf. Radical of rings and algebras) [1].

There is the following generalization of the concept of a prime ring. A ring is said to be semi-prime if it does not have non-zero nilpotent ideals.

References

[1]	V.A. Andrunakievich, Yu.M. Ryabukhin, "Radicals of algebras and lattice theory" , Moscow (1979) (In Russian)
[2]	N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956)
[3]	I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968)