CR-submanifold
Let 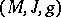 be an almost Hermitian manifold (cf. also Hermitian structure), where
be an almost Hermitian manifold (cf. also Hermitian structure), where 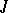 is an almost-complex structure on
is an almost-complex structure on  and
and 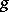 is a Riemannian metric on
is a Riemannian metric on  satisfying
satisfying 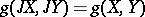 for any vector fields
for any vector fields 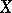 and
and 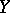 on
on  . A real submanifold
. A real submanifold  of
of 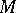 is said to be a complex (holomorphic) submanifold if the tangent bundle
is said to be a complex (holomorphic) submanifold if the tangent bundle 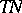 of
of 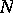 is invariant under
is invariant under 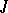 , i.e.
, i.e. 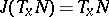 for any
for any 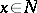 . Let
. Let 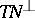 be the normal bundle of
be the normal bundle of 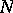 . Then
. Then 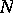 is called a totally real (anti-invariant) submanifold if
is called a totally real (anti-invariant) submanifold if  for any
for any 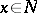 .
.
In 1978, A. Bejancu [a1] introduced the notion of a CR-submanifold as a natural generalization of both complex submanifolds and totally real submanifolds. More precisely, 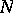 is said to be a CR-submanifold if there exists a smooth distribution
is said to be a CR-submanifold if there exists a smooth distribution 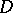 on
on 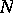 such that:
such that:
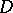 is a holomorphic distribution, that is,
is a holomorphic distribution, that is,  for any
for any 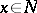 ;
;
the complementary orthogonal distribution 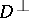 of
of  is a totally real distribution, that is,
is a totally real distribution, that is, 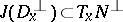 for any
for any 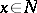 .
.
The above concept has been mainly investigated from the viewpoint of differential geometry (cf. [a2], [a3], [a5], [a6], [a7]).
Let 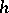 be the second fundamental form of the CR-submanifold
be the second fundamental form of the CR-submanifold  . Then one says that
. Then one says that  is
is 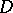 -geodesic,
-geodesic, 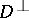 -geodesic or mixed geodesic if
-geodesic or mixed geodesic if 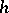 vanishes on
vanishes on 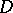 or
or 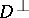 , or
, or 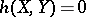 for any
for any 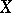 in
in  and
and 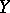 in
in 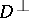 , respectively.
, respectively.
From the viewpoint of complex analysis, a CR-submanifold is an imbedded CR-manifold in a complex manifold. In this case a real hypersurface 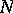 of a complex manifold
of a complex manifold 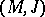 is a CR-submanifold (cf. [a4]).
is a CR-submanifold (cf. [a4]).
References
| [a1] | A. Bejancu, "CR submanifolds of a Kaehler manifold I" Proc. Amer. Math. Soc. , 69 (1978) pp. 134–142 |
| [a2] | A. Bejancu, "Geometry of CR submanifolds" , Reidel (1986) |
| [a3] | D.E. Blair, B.Y. Chen, "On CR submanifolds of Hermitian manifolds" Israel J. Math. , 34 (1979) pp. 353–363 |
| [a4] | A. Boggess, "CR manifolds and tangential Cauchy–Riemann complex" , CRC (1991) |
| [a5] | B.Y. Chen, "Geometry of submanifolds and its applications" , Tokyo Sci. Univ. (1981) |
| [a6] | K. Yano, M. Kon, "CR submanifolds of Kaehlerian and Sasakian manifolds" , Birkhäuser (1983) |
| [a7] | K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984) |
CR-submanifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=CR-submanifold&oldid=16186