Genus of a surface
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A numerical birational invariant of a two-dimensional algebraic variety defined over an algebraically closed field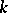 
. There are two different genera — the arithmetic genus and the geometric genus. The geometric genus 
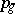of a complete smooth algebraic surface 
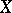is equal to
 |
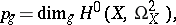i.e. to the dimension of the space of regular differential 
-forms (cf. Differential form) on 
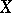. The arithmetic genus 
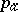of a complete smooth algebraic surface 
is equal to
 |
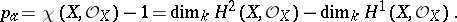The geometric and arithmetic genera of a complete smooth algebraic surface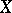 
are related by the formula 
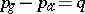, where 
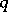is the irregularity of 
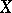, which is equal to the dimension of the space of regular differential 
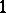-forms on 
.
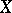References
| [1] | I.R., et al. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [a2] | A. van de Ven, "Compact complex surfaces" , Springer (1984) |
| [a3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
How to Cite This Entry:
Genus of a surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_a_surface&oldid=16127
Genus of a surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Genus_of_a_surface&oldid=16127
This article was adapted from an original article by Vik.S. Kulikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article