Locally flat imbedding

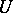An imbedding (cf. Immersion) of one topological manifold into another such that for any point there are charts in a neighbourhood of and in a neighbourhood of the point in in which the restriction of to linearly maps to 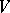. In other words, is locally linear in suitable coordinate systems. Equivalently: There are neighbourhoods 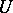of a point and of the point 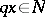such that the pair can be mapped homeomorphically onto a standard pair or 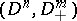, where 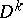is the unit ball of the space 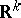with centre at the origin and is the intersection of this ball with the half-space .

Any imbedding of a circle and an arc into a plane is locally flat; however, a circle or an arc can be imbedded in 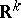with 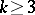in a manner that is not locally flat (see Wild imbedding; Wild sphere). Any smooth imbedding is locally flat in the smooth sense (that is, in the definition the coordinates can be chosen to be smooth). A piecewise-linear imbedding need not be locally flat, not only in the piecewise-linear sense, but even not in the topological sense; for example, a cone with vertex in 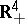over a closed polygon knotted in the bounding plane 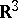. 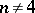For and 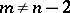there is a homotopy criterion for an imbedding to be locally flat: For every point and neighbourhood of the point there is a neighbourhood 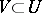such that any loop in 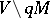is homotopic to zero in 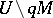(local simple connectedness). If 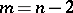, then such a criterion holds for 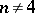, but is essentially more complicated. For the question remains unsettled (1989). For 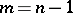and 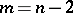a locally flat imbedding has a topological normal bundle.

References

[a1]	J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , Topology of manifolds , Markham (1970)