Schubert polynomials

Polynomials introduced by A. Lascoux and M.-P. Schützenberger [a18] as distinguished polynomial representatives of Schubert cycles (cf. also Schubert cycle) in the cohomology ring of the manifold of complete flags in . This extended work by I.N. Bernshtein, I.M. Gel'fand and S.I. Gel'fand [a1] and M. Demazure [a8], who gave algorithms for computing representatives of Schubert cycles in the co-invariant algebra, which is isomorphic to the cohomology ring of [a6]:

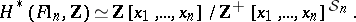Here, is the ideal generated by the non-constant polynomials that are symmetric in . See [a19] for an elegant algebraic treatment of Schubert polynomials, and [a13] and [a20] for a more geometric treatment.

For each , let 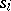be the transposition in the symmetric group 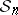, which acts on 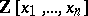. The divided difference operator 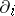is defined by

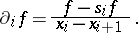These satisfy

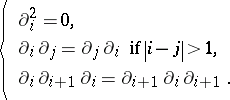(a1)

If 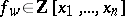is a representative of the Schubert cycle 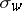, then

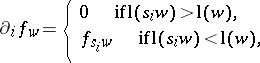where is the length of a permutation 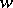and 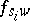represents the Schubert cycle . Given a fixed polynomial representative of the Schubert cycle 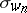(the class of a point as 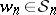is the longest element), successive application of divided difference operators gives polynomial representatives of all Schubert cycles, which are independent of the choices involved, by (a1).

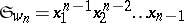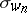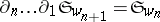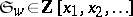The choice of the representative for gives the Schubert polynomials. Since , Schubert polynomials are independent of and give polynomials for 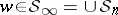. These form a basis for this polynomial ring, and every Schur polynomial is also a Schubert polynomial.

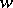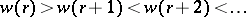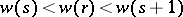The transition formula gives another recursive construction of Schubert polynomials. For , let be the last descent of () and define by . Set 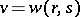, where is the transposition. Then

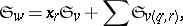the sum over all 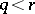with 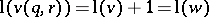. This formula gives an algorithm to compute 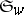as the permutations that appear on the right-hand side are either shorter than 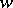or precede it in reverse lexicographic order, and the minimal such permutation of length 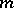has .

The transition formula shows that the Schubert polynomial 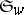is a sum of monomials with non-negative integral coefficients. There are several explicit formulas for the coefficient of a monomial in a Schubert polynomial, either in terms of the weak order of the symmetric group [a3], [a5], [a12], an intersection number [a15] or the Bruhat order [a4]. An elegant conjectural formula of A. Kohnert [a16] remains unproven (as of 2000). The Schubert polynomial 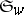for is also the normal form reduction of any polynomial representative of the Schubert cycle 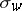with respect to the degree-reverse lexicographic term order on with .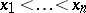

The above-mentioned results of [a6], [a1], [a8] are valid more generally for any flag manifold with 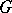a semi-simple reductive group and 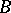a Borel subgroup. When 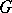is an orthogonal or symplectic group, there are competing theories of Schubert polynomials [a2], [a10], [a17], each with own merits. There are also double Schubert polynomials suited for computations of degeneracy loci [a11], quantum Schubert polynomials [a9], [a7] and universal Schubert polynomials [a14].

References

[a1]	I.N. Bernshtein, I.M. Gel'fand, S.I. Gel'fand, "Schubert cells and cohomology of the spaces 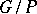" Russian Math. Surveys , 28 : 3 (1973) pp. 1–26
[a2]	S. Billey, M. Haiman, "Schubert polynomials for the classical groups" J. Amer. Math. Soc. , 8 : 2 (1995) pp. 443–482
[a3]	S. Billey, W. Jockush, R. Stanley, "Some combinatorial properties of Schubert polynomials" J. Algebraic Combin. , 2 : 4 (1993) pp. 345–374
[a4]	N. Bergeron, F. Sottile, "Skew Schubert functions and the Pieri formula for flag manifolds" Trans. Amer. Math. Soc. (to appear)
[a5]	N. Bergeron, "A combinatorial construction of the Schubert polynomials" J. Combin. Th. A , 60 (1992) pp. 168–182
[a6]	A. Borel, "Sur la cohomologie des espaces fibrés principaux et des espaces homogènes des groupes de Lie compacts" Ann. Math. , 57 (1953) pp. 115–207
[a7]	I. Ciocan–Fontanine, "On quantum cohomology rings of partial flag varieties" Duke Math. J. , 98 : 3 (1999) pp. 485–524
[a8]	M. Demazure, "Désingularization des variétés de Schubert généralisées" Ann. Sci. École Norm. Sup. (4) , 7 (1974) pp. 53–88
[a9]	S. Fomin, S. Gelfand, A. Postnikov, "Quantum Schubert polynomials" J. Amer. Math. Soc. , 10 (1997) pp. 565–596
[a10]	S. Fomin, A.N. Kirillov, "Combinatorial 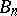-analogs of Schubert polynomials" Trans. Amer. Math. Soc. , 348 (1996) pp. 3591–3620
[a11]	W. Fulton, P. Pragacz, "Schubert varieties and degeneracy loci" , Lecture Notes in Mathematics , 1689 , Springer (1998)
[a12]	S. Fomin, R. Stanley, "Schubert polynomials and the nilCoxeter algebra" Adv. Math. , 103 (1994) pp. 196–207
[a13]	W. Fulton, "Young tableaux" , Cambridge Univ. Press (1997)
[a14]	W. Fulton, "Universal Schubert polynomials" Duke Math. J. , 96 : 3 (1999) pp. 575–594
[a15]	A. Kirillov, T. Maeno, "Quantum double Schubert polynomials, quantum Schubert polynomials, and the Vafa–Intriligator formula" Discr. Math. , 217 : 1–3 (2000) pp. 191–223 (Formal Power Series and Algebraic Combinatorics (Vienna, 1997))
[a16]	A. Kohnert, "Weintrauben, polynome, tableaux" Bayreuth Math. Schrift. , 38 (1990) pp. 1–97
[a17]	A. Lascoux, P. Pragacz, J. Ratajski, "Symplectic Schubert polynomials à la polonaise, appendix to operator calculus for 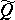-polynomials and Schubert polynomials" Adv. Math. , 140 (1998) pp. 1–43
[a18]	A. Lascoux, M.-P. Schützenberger, "Polynômes de Schubert" C.R. Acad. Sci. Paris , 294 (1982) pp. 447–450
[a19]	I.G. Macdonald, "Notes on Schubert polynomials" Lab. Combin. et d'Inform. Math. (LACIM) Univ. Québec (1991)
[a20]	L. Manivel, "Fonctions symétriques, polynômes de Schubert et lieux de dégénérescence" Cours Spécialisés Soc. Math. France , 3 (1998)