Polynomial convexity
Let 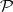 denote the set of holomorphic polynomials on
denote the set of holomorphic polynomials on 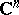 (cf. also Analytic function). Let
(cf. also Analytic function). Let 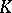 be a compact set in
be a compact set in 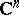 and let
and let 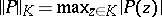 be the sup-norm of
be the sup-norm of 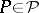 on
on 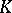 . The set
. The set
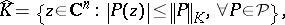 |
is called the polynomially convex hull of 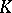 . If
. If 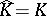 one says that
one says that 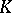 is polynomially convex.
is polynomially convex.
An up-to-date (as of 1998) text dealing with polynomial convexity is [a3], while [a13] and [a27] contain some sections on polynomial convexity, background and older results. The paper [a24] is an early study on polynomial convexity.
Polynomial convexity arises naturally in the context of function algebras (cf. also Algebra of functions): Let 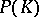 denote the uniform algebra generated by the holomorphic polynomials on
denote the uniform algebra generated by the holomorphic polynomials on 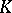 with the sup-norm. The maximal ideal space
with the sup-norm. The maximal ideal space 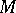 of
of 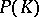 is the set of homomorphisms mapping
is the set of homomorphisms mapping 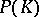 onto
onto 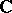 , endowed with the topology inherited from the dual space
, endowed with the topology inherited from the dual space 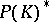 . It can be identified with
. It can be identified with 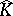 via
via
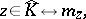 |
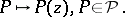 |
Moreover, if 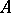 is any finitely generated function algebra on a compact Hausdorff space, then
is any finitely generated function algebra on a compact Hausdorff space, then 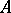 is isomorphic to
is isomorphic to 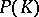 , where for
, where for 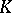 one can take the joint spectrum of the generators of
one can take the joint spectrum of the generators of 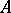 (cf. also Spectrum of an operator).
(cf. also Spectrum of an operator).
By the Riesz representation theorem (cf. Riesz theorem) there exists for every  at least one representing measure
at least one representing measure 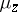 , that is, a probability measure
, that is, a probability measure 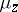 on
on 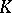 such that
such that
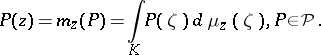 |
One calls 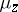 a Jensen measure if it has the stronger property
a Jensen measure if it has the stronger property
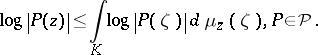 |
It can be shown that for each 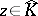 there exists a Jensen measure
there exists a Jensen measure  . See e.g. [a27].
. See e.g. [a27].
For compact sets 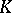 in
in 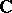 one obtains
one obtains 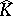 by "filling in the holes" of
by "filling in the holes" of 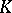 , that is,
, that is,  , where
, where 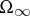 is the unbounded component of
is the unbounded component of 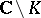 . In
. In 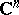 ,
, 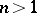 , there is no such a simple topological description.
, there is no such a simple topological description.
Early results on polynomial convexity, cf. [a13], are
Oka's theorem: If 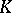 is a polynomially convex set in
is a polynomially convex set in 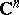 and
and 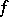 is holomorphic on a neighbourhood of
is holomorphic on a neighbourhood of  , then
, then 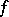 can be written on
can be written on 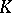 as a uniform limit of polynomials. Cf. also Oka theorems.
as a uniform limit of polynomials. Cf. also Oka theorems.
Browder's theorem: If 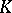 is polynomially convex in
is polynomially convex in  , then
, then 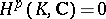 for
for 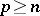 .
.
Here, 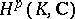 is the
is the 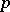 th Čech cohomology group. More recently (1994), the following topological result was obtained, cf. [a9], [a3]:
th Čech cohomology group. More recently (1994), the following topological result was obtained, cf. [a9], [a3]:
Forstnerič' theorem: Let 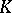 be a polynomially convex set in
be a polynomially convex set in  ,
, 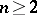 . Then
. Then
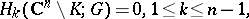 |
and
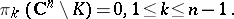 |
Here, 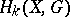 denotes the
denotes the 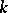 th homology group of
th homology group of 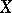 with coefficients in an Abelian group
with coefficients in an Abelian group 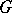 and
and 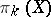 is the
is the  th homotopy group of
th homotopy group of 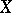 .
.
One method to find 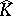 is by means of analytic discs. Let
is by means of analytic discs. Let 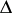 be the unit disc in
be the unit disc in 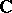 and let
and let 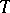 be its boundary. An analytic disc is (the image of) a holomorphic mapping
be its boundary. An analytic disc is (the image of) a holomorphic mapping 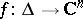 such that
such that 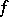 is continuous up to
is continuous up to 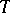 . Similarly one defines an
. Similarly one defines an 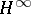 -disc as a bounded holomorphic mapping
-disc as a bounded holomorphic mapping 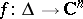 . Its components are elements of the usual Hardy space
. Its components are elements of the usual Hardy space  (cf. Hardy spaces).
(cf. Hardy spaces).
Now, let 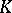 be compact in
be compact in 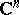 and suppose that
and suppose that 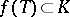 for some analytic disc
for some analytic disc 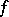 . Then
. Then 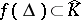 by the maximum principle applied to
by the maximum principle applied to 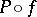 for polynomials
for polynomials 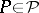 . The same goes for
. The same goes for 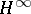 -discs whose boundary values are almost everywhere in
-discs whose boundary values are almost everywhere in 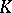 . One says that the disc
. One says that the disc 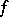 is glued to
is glued to 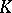 . Next, one says that
. Next, one says that 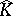 has analytic structure at
has analytic structure at 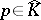 if there exists a non-constant analytic disc
if there exists a non-constant analytic disc  such that
such that 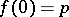 and the image of
and the image of 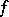 is contained in
is contained in 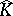 .
.
It was a major question whether 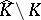 always has analytic structure. Moreover, when is
always has analytic structure. Moreover, when is 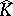 obtained by glueing discs to
obtained by glueing discs to 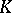 ? One positive result in this direction is due to H. Alexander [a1]; a corollary of his work is as follows: If
? One positive result in this direction is due to H. Alexander [a1]; a corollary of his work is as follows: If 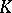 is a rectifiable curve in
is a rectifiable curve in 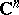 , then either
, then either 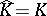 and
and 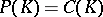 , or
, or 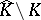 is a pure
is a pure 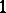 -dimensional analytic subset of
-dimensional analytic subset of 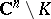 (cf. also Analytic set). If
(cf. also Analytic set). If 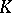 is a rectifiable arc,
is a rectifiable arc, 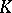 is polynomially convex and
is polynomially convex and 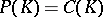 .
.
See [a1] for the complete formulation. Alexander's result is an extension of pioneering work of J. Wermer, cf. [a30], E. Bishop and, later, G. Stolzenberg [a26], who dealt with real-analytic, respectively 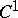 , curves. Wermer [a29] gave the first example of an arc in
, curves. Wermer [a29] gave the first example of an arc in 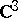 that is not polynomially convex, cf. [a3]. However, Gel'fand's problem (i.e., let
that is not polynomially convex, cf. [a3]. However, Gel'fand's problem (i.e., let 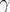 be an arc in
be an arc in 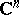 such that
such that 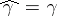 ; is it true that
; is it true that 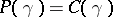 ?) is still open (2000). Under the additional assumption that its projections into the complex coordinate planes have
?) is still open (2000). Under the additional assumption that its projections into the complex coordinate planes have  -dimensional Hausdorff measure
-dimensional Hausdorff measure  , the answer is positive, see [a3].
, the answer is positive, see [a3].
F.R. Harvey and H.B. Lawson gave a generalization to higher-dimensional 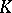 , cf. [a12], which includes the following.
, cf. [a12], which includes the following.
Let 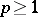 . If
. If 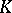 is a
is a 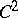
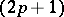 -dimensional submanifold of
-dimensional submanifold of 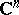 and at each point of
and at each point of 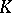 the tangent space to
the tangent space to 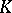 contains a
contains a  -dimensional complex subspace, then
-dimensional complex subspace, then 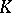 is the boundary of an analytic variety (in the sense of Stokes' theorem).
is the boundary of an analytic variety (in the sense of Stokes' theorem).
Another positive result is contained in the work of E. Bedford and W. Klingenberg, cf. [a4]: Suppose 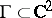 is the graph of a
is the graph of a 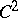 -function
-function 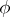 over the boundary of a strictly convex domain
over the boundary of a strictly convex domain 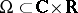 . Then
. Then 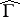 is the graph of a Lipschitz-continuous extension
is the graph of a Lipschitz-continuous extension 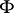 of
of 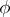 on
on  . Moreover,
. Moreover, 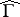 is foliated with analytic discs (cf. also Foliation).
is foliated with analytic discs (cf. also Foliation).
The work of Bedford and Klingenberg has been generalized in various directions in [a16], [a21] and [a7]. One ingredient of this theorem is work of Bishop [a5], which gives conditions that guarantee locally the existence of analytic discs with boundary in real submanifolds of sufficiently high dimension. See [a11], [a32] and [a15] for results along this line.
A third situation that is fairly well understood is when 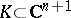 is a compact set fibred over
is a compact set fibred over 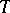 , that is,
, that is, 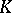 is of the form
is of the form 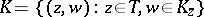 , where
, where 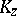 is a compact set in
is a compact set in 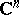 depending on
depending on  .
.
In this case the following is true: Let 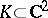 be a compact fibration over the circle
be a compact fibration over the circle 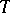 and suppose that for each
and suppose that for each  the fibre
the fibre 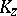 is connected and simply connected. Then
is connected and simply connected. Then 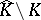 is the union of graphs
is the union of graphs 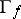 , where
, where 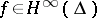 and the boundary values
and the boundary values 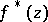 are in
are in  for almost all
for almost all 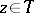 .
.
Of course, it is possible that 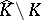 is empty. The present theorem is due to Z. Slodkowski, [a22], earlier results are in [a2] and [a10]. Slodkowski proved a similar theorem in
is empty. The present theorem is due to Z. Slodkowski, [a22], earlier results are in [a2] and [a10]. Slodkowski proved a similar theorem in 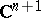 under the assumption that the fibres are convex, see [a23].
under the assumption that the fibres are convex, see [a23].
Despite these positive results, in general 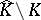 need not have analytic structure. This has become clear from examples by Stolzenberg [a25] and Wermer [a31]. Presently (2000) it is not known whether
need not have analytic structure. This has become clear from examples by Stolzenberg [a25] and Wermer [a31]. Presently (2000) it is not known whether 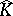 has analytic structure everywhere if
has analytic structure everywhere if 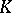 is a (real) submanifold of
is a (real) submanifold of  , nor is it known under what conditions
, nor is it known under what conditions 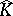 is obtained by glueing discs to
is obtained by glueing discs to 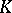 .
.
However, it has been shown that in a weaker sense there is always a kind of analytic structure in polynomial hulls. Let 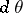 denote Lebesgue measure on the circle
denote Lebesgue measure on the circle  and let
and let 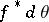 denote the push-forward of
denote the push-forward of 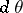 under a continuous mapping
under a continuous mapping 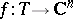 . Let also
. Let also 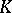 be a compact set in
be a compact set in 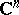 . The following are equivalent:
. The following are equivalent:
1) 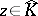 and
and 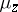 is a Jensen measure for
is a Jensen measure for  supported on
supported on 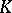 ;
;
2) There exists a sequence of analytic discs 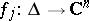 such that
such that 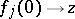 and
and 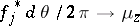 in the weak-
in the weak- sense (cf. also Weak topology).
sense (cf. also Weak topology).
This was proved in [a6]; [a8] and [a20] contain more information about additional nice properties that can be required from the sequence of analytic discs. Under suitable regularity conditions on 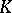 , it is shown in [a19] that
, it is shown in [a19] that  consists of analytic discs
consists of analytic discs 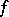 such that
such that 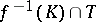 has Lebesgue measure arbitrary close to
has Lebesgue measure arbitrary close to 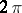 .
.
Another problem is to describe  assuming that
assuming that 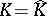 and given reasonable additional conditions on
and given reasonable additional conditions on 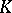 . In particular, when can one conclude that
. In particular, when can one conclude that 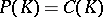 ? Recall that a real submanifold
? Recall that a real submanifold 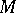 of
of 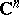 is totally real at
is totally real at 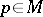 if the tangent space in
if the tangent space in 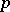 does not contain a complex line (cf. also CR-submanifold). The Hörmander–Wermer theorem is as follows, cf. [a14]: Let
does not contain a complex line (cf. also CR-submanifold). The Hörmander–Wermer theorem is as follows, cf. [a14]: Let 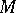 be a sufficiently smooth real submanifold of
be a sufficiently smooth real submanifold of  and let
and let  be the subset of
be the subset of 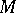 consisting of points that are not totally real. If
consisting of points that are not totally real. If 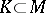 is a compact polynomially convex set that contains an
is a compact polynomially convex set that contains an 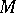 -neighbourhood of
-neighbourhood of 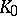 , then
, then  contains all continuous functions on
contains all continuous functions on  that are on
that are on 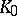 the uniform limit of functions holomorphic in a neighbourhood of
the uniform limit of functions holomorphic in a neighbourhood of 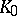 .
.
See [a17] for a variation on this theme. One can deal with some situations where the manifold is replaced by a union of manifolds; e.g., B.M. Weinstock [a28] gives necessary and sufficient conditions for any compact subset of the union of two totally real  -dimensional subspaces of
-dimensional subspaces of  to be polynomially convex; then also
to be polynomially convex; then also 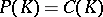 . See also [a18].
. See also [a18].
References
| [a1] | H. Alexander, "Polynomial approximation and hulls in sets of finite linear measure in 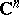 " Amer J. Math. , 62 (1971) pp. 65–74 " Amer J. Math. , 62 (1971) pp. 65–74 |
| [a2] | H. Alexander, J. Wermer, "Polynomial hulls with convex fibres" Math. Ann. , 281 (1988) pp. 13–22 |
| [a3] | H. Alexander, J. Wermer, "Several complex variables and Banach algebras" , Springer (1998) |
| [a4] | E. Bedford, W. Klingenberg Jr., "On the envelope of holomorphy of a  -sphere in -sphere in 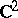 " J. Amer. Math. Soc. , 4 (1991) pp. 623–646 " J. Amer. Math. Soc. , 4 (1991) pp. 623–646 |
| [a5] | E. Bishop, "Differentiable manifolds in Euclidean space" Duke Math. J. , 32 (1965) pp. 1–21 |
| [a6] | S. Bu, W. Schachermayer, "Approximation of Jensen measures by image measures under holomorphic functions and applications" Trans. Amer. Math. Soc. , 331 (1992) pp. 585–608 |
| [a7] | E.M. Chirka, N.V. Shcherbina, "Pseudoconvexity of rigid domains and foliations of hulls of graphs" Ann. Scuola Norm. Sup. Pisa , 22 (1995) pp. 707–735 |
| [a8] | J. Duval, N. Sibony, "Polynomial convexity, rational convexity and currents" Duke Math. J. , 79 (1995) pp. 487–513 |
| [a9] | F. Forstnerič, "Complements of Runge domains and holomorphic hulls" Michigan Math. J. , 41 (1994) pp. 297–308 |
| [a10] | F. Forstnerič, "Polynomial hulls of sets fibered over the circle" Indiana Univ. Math. J. , 37 (1988) pp. 869–889 |
| [a11] | F. Forstnerič, E.L. Stout, "A new class of polynomially convex sets" Ark. Mat. , 29 (1991) pp. 51–62 |
| [a12] | F.R. Harvey, H.B. Lawson Jr., "On boundaries of complex analytic varieties I" Ann. of Math. , 102 (1975) pp. 223–290 |
| [a13] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
| [a14] | L. Hörmander, J. Wermer, "Uniform approximation on compact sets in 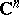 " Math. Scand. , 23 (1968) pp. 5–21 " Math. Scand. , 23 (1968) pp. 5–21 |
| [a15] | B. Jöricke, "Local polynomial hulls of discs near isolated parabolic points" Indiana Univ. Math. J. , 46 : 3 (1997) pp. 789–826 |
| [a16] | N.G. Kruzhilin, "Two-dimensional spheres in the boundaries of strictly pseudoconvex domains in 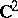 " Math. USSR Izv. , 39 (1992) pp. 1151–1187 (In Russian) " Math. USSR Izv. , 39 (1992) pp. 1151–1187 (In Russian) |
| [a17] | A.G. O'Farrell, K.J. Preskenis, D. Walsh, "Holomorphic approximation in Lipschitz norms" , Proc. Conf. Banach Algebras and Several Complex Variables (New Haven, Conn., 1983) , Contemp. Math. , 32 (1983) pp. 187–194 |
| [a18] | P.J. de Paepe, "Approximation on a disk I" Math. Z. , 212 (1993) pp. 145–152 |
| [a19] | E.A. Poletsky, "Holomorphic currents" Indiana Univ. Math. J. , 42 (1993) pp. 85–144 |
| [a20] | E.A. Poletsky, "Analytic geometry on compacta in 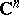 " Math. Z. , 222 (1996) pp. 407–424 " Math. Z. , 222 (1996) pp. 407–424 |
| [a21] | N. Shcherbina, "On the polynomial hull of a graph" Indiana Univ. Math. J. , 42 (1993) pp. 477–503 |
| [a22] | Z. Slodkowski, "Polynomial hulls with convex convex sections and interpolating spaces" Proc. Amer. Math. Soc. , 96 (1986) pp. 255–260 |
| [a23] | Z. Slodkowski, "Polynomial hulls in 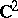 and quasi circles" Ann. Scuola Norm. Sup. Pisa , 16 (1989) pp. 367–391 and quasi circles" Ann. Scuola Norm. Sup. Pisa , 16 (1989) pp. 367–391 |
| [a24] | G. Stolzenberg, "Polynomially and rationally convex sets" Acta Math. , 109 (1963) pp. 259–289 |
| [a25] | G. Stolzenberg, "A hull with no analytic structure" J. Math. Mech. , 12 (1963) pp. 103–112 |
| [a26] | G. Stolzenberg, "Uniform approximation on smooth curves" Acta Math. , 115 (1966) pp. 185–198 |
| [a27] | E.L. Stout, "The theory of uniform algebras" , Bogden and Quigley (1971) |
| [a28] | B.M. Weinstock, "On the polynomial convexity of the union of two maximal totally real subspaces of  " Math. Ann. , 282 (1988) pp. 131–138 " Math. Ann. , 282 (1988) pp. 131–138 |
| [a29] | J. Wermer, "Polynomial approximation on an arc in 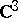 " Ann. of Math. , 62 (1955) pp. 269–270 " Ann. of Math. , 62 (1955) pp. 269–270 |
| [a30] | J. Wermer, "The hull of a curve in 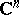 " Ann. of Math. , 68 (1958) pp. 550–561 " Ann. of Math. , 68 (1958) pp. 550–561 |
| [a31] | J. Wermer, "On an example of Stolzenberg" , Symp. Several Complex Variables, Park City, Utah , Lecture Notes in Mathematics , 184 , Springer (1970) |
| [a32] | J. Wiegerinck, "Local polynomially convex hulls at degenerated CR singularities of surfaces in 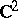 " Indiana Univ. Math. J. , 44 (1995) pp. 897–915 " Indiana Univ. Math. J. , 44 (1995) pp. 897–915 |
Polynomial convexity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polynomial_convexity&oldid=14374