Integral sine
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The special function defined for real  by
by
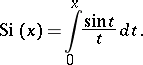 |
For  one has
one has
 |
One sometimes uses the notation
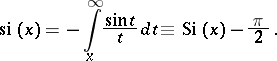 |
Some particular values are:
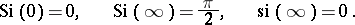 |
Some special relations:
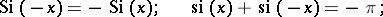 |
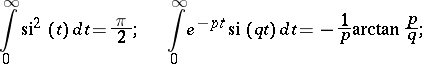 |
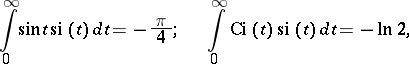 |
where  is the integral cosine. For
is the integral cosine. For  small,
small,
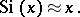 |
The asymptotic representation for large  is
is
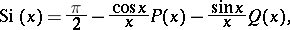 |
where
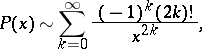 |
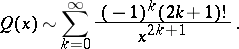 |
The integral sine has the series representation
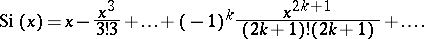 | (*) |
As a function of the complex variable  ,
, 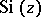 , defined by (*), is an entire function of
, defined by (*), is an entire function of  in the
in the  -plane.
-plane.
The integral sine is related to the integral exponential function  by
by
 |
See also Si-ci-spiral.
For references, and the graph of the integral sine, see Integral cosine.
Comments
This function is better known as the sine integral.
How to Cite This Entry:
Integral sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_sine&oldid=11622
Integral sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_sine&oldid=11622
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article