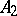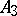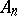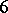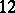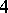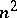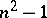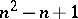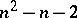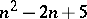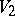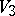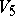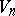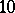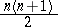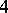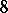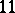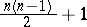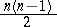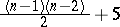Lacunary space

A space with an affine connection or a Riemannian space of some definite "degree of mobility of a space with an affine connectiondegree of mobility" . A lacunary space is defined by the order of the complete group of motions, that is, by the largest number of parameters of that group for the given space. Thus, ordinary $n$-dimensional affine space admits a group of motions of maximal order $n^2+n$.

<tbody> </tbody> Types of spaces and lacunae Spaces of first lacunarity First lacuna Spaces of second lacunarity 1 1 Second lacuna Spaces of third lacunarity Third lacuna Spaces of fourth lacunarity 3 2 1

The orders of the complete groups of motions of other spaces with an affine connection belong to the interval of natural numbers , but not every number of this interval can be the order of a complete group of motions. Intervals of greatest length composed of numbers that are not the order of a complete group of motions are called lacunae, and the complements of them with respect to the given interval are called intervals of condensation. A space is called a space of -th lacunarity if the order of its complete group of motions belongs to the interval of condensation having number . The calculation is carried out with an interval of condensation containing the maximal order. For the well-known distribution of the number of motions of "rigid" bodies in spaces with an affine connection see Table 1. It deals with the orders of complete groups of motions — synonyms for the degree of mobility or the degree of freedom of rigid bodies. The question of determining the possible degrees of mobility of rigid and similarly varying bodies in Riemannian spaces has been partly solved for spaces with a metric of fixed sign only. In the general case the degrees of mobility and the Riemannian spaces realizing them that are known are exhibited in Table 2.

<tbody> </tbody> Types of spaces and lacunae 15 Spaces of first lacunarity (constant curvature) First lacuna Spaces of second lacunarity 1 Second lacuna Spaces of third lacunarity 3 2 1

References

[1]	I.P. Egorov, "Motions in generalized differential-geometric spaces" Progress in Math. , 6 (1970) pp. 171–228 Itogi Nauk. Algebra Topol. Geom. 1965 (1967) pp. 375–428
[2]	I.P. Egorov, "Automorphisms in generalized spaces" J. Soviet Math. , 14 (1980) pp. 1260–1287 Itogi Nauk. i Tekhn. Probl. Geom. , 10 (1978) pp. 147–191
[3]	I.P. Egorov, "Geometry" , Moscow (1979) (In Russian)

Comments

The Riemannian manifolds of dimension with group of isometries of (the maximal) dimension are -dimensional Euclidean space, the -dimensional sphere , -dimensional real projective space , and an -dimensional simply-connected hyperbolic space.

For a list of Riemannian manifolds of dimension with a "degree of mobility" at least , and the corresponding groups cf. [a1], p. 54.

At the other end of the scale there is, for example, the theorem of Bochner, [a4], that if is a compact Riemannian manifold with negative Ricci tensor, then its group of isometries is finite.

Let be a manifold of dimension . For each Riemannian metric let 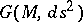be the group of isometries of . The degree of symmetry of 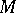is the maximum of the .

For a description of the possible isometry groups of dimensions cf. [a2], [a3].

References

[a1]	S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972)
[a2]	S. Kobayashi, T. Nagano, "Riemannian manifolds with abundant symmetries" , Differential geometry (in honor of K. Yano) , Kinokuniya (1972) pp. 195–220
[a3]	H. Wakakuwa, "On $n$-dimensional Riemannian spaces admitting some groups of motions of order less than $n(n-1)/2$" Tôhoku Math. J. , 6 (1954) pp. 121–134
[a4]	S. Bochner, "Vector fields and Ricci curvature" Bull. Amer. Math. Soc. , 52 (1946) pp. 776–797