Dispersion relation

A relation connecting certain magnitudes which characterize the scattering of particles with magnitudes characterizing their absorption. More exactly, the dispersion relation is a relation connecting the real part of the scattering amplitude (in the more general case, the Green function) with certain types of integrals of its imaginary part. Let a function $ f ( t) $ be absolutely integrable on the axis, and let it satisfy the causal relation $ f ( t) = 0 $, $ t < 0 $. Then its Fourier–Laplace transform

$$ \widetilde{f} ( \zeta ) = \int\limits f ( t) e ^ {i \zeta t } dt , \ \zeta = p + iq , $$

will be a holomorphic function in the upper half-plane $ q > 0 $, and the real and imaginary parts of the boundary value $ \widetilde{f} ( p) $ will satisfy the dispersion relation

$$ \tag{* } \mathop{\rm Re} \widetilde{f} ( p) = \frac{1} \pi v _ {p} \int\limits _ {- \infty } ^ \infty \frac{ \mathop{\rm Im} \widetilde{f} ( p ^ \prime ) d p ^ \prime }{p ^ \prime - p } . $$

In describing real physical processes the dispersion relation of the type (*) becomes more complicated, since the function $ \widetilde{f} ( \zeta ) $ may increase at infinity as a polynomial (in this case a dispersion relation with subtractions is obtained), the boundary value $ \widetilde{f} ( p) $ may be a generalized function of slow growth, while the number of variables may be more than one (multi-dimensional dispersion relations).

References

[1]	N.N. Bogolyubov, B.V. Medvedev, M.K. Polivanov, "Questions in the theory of dispersion relations" , Moscow (1958) (In Russian)
[2]	V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian)
[3]	N.N. Bogolyubov, A.A. Logunov, A.I. Oksak, I.T. Todorov, "General principles of quantum field theory" , Kluwer (1990) (Translated from Russian)

Comments

A dispersion relation of the type defined here is often called a Kramers–Kronig relation. In the classical dispersion of light the relation gives a connection between the real (dispersive) and imaginary (absorptive) parts of the index of refraction.

Consider a linear wave equation such as the beam equation $ \phi _ {tt} + \gamma ^ {2} \phi _ {xxxx} = 0 $. For a sinusoidal wave train $ \phi ( x , t ) = A \mathop{\rm exp} ( i k \cdot x - i \omega t ) $ to satisfy such an equation some relation $ G ( k , \omega ) = 0 $ between the frequency and the wave number must hold. In this case $ \omega ^ {2} - \gamma ^ {2} k ^ {4} = 0 $. This relation is called the dispersion relation. There are generalizations to non-linear wave equations, e.g., the KdV-equation, where the dispersion relation also involves the amplitude. Dispersion relations for waves are extensively discussed in [a5].

References

[a1]	R. Kronig, J Opt. Soc. Amer , 12 (1926) pp. 547
[a2]	H.A. Kramers, , Atti. Congr. Intern. Fisici Como , 2 (1927) pp. 545
[a3]	N.G. van Kampen, "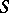-matrix and causality condition I. Maxwell field" Phys. Rev. , 89 (1953) pp. 1072–1079
[a4]	N.G. van Kampen, "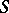-matrix and causality condition II. Nonrelativistic particles" Phys. Rev. , 91 (1953) pp. 1267–1276
[a5]	H. Bremermann, "Distributions, complex variables, and Fourier transforms" , Addison-Wesley (1965)
[a6]	G.B. Whitham, "Linear and non-linear waves" , Wiley (1974)