Cohomology of groups

Historically, the earliest theory of a cohomology of algebras.

With every pair $( G, A)$, where $G$ is a group and $A$ a left $G$- module (that is, a module over the integral group ring $\mathbf Z G$), there is associated a sequence of Abelian groups $H ^ { n } ( G, A)$, called the cohomology groups of $G$ with coefficients in $A$. The number $n$, which runs over the non-negative integers, is called the dimension of $H ^ { n } ( G, A)$. The cohomology groups of groups are important invariants containing information both on the group $G$ and on the module $A$.

By definition, $H ^ {0} ( G, A)$ is $\mathop{\rm Hom} _ {G} ( \mathbf Z , A) \simeq A ^ {G}$, where $A ^ {G}$ is the submodule of $G$- invariant elements in $A$. The groups $H ^ { n } ( G, A)$, $n > 1$, are defined as the values of the $n$- th derived functor of the functor $A \mapsto H ^ {0} ( G, A)$. Let

$$\dots \rightarrow ^ { {d _ n} } \ P _ {n} \rightarrow ^ { {d _ {n} - 1 } } \ P _ {n - 1 } \rightarrow \dots \rightarrow \ P _ {0} \rightarrow \mathbf Z \rightarrow 0$$

be some projective resolution of the trivial $G$- module $\mathbf Z$ in the category of $G$- modules, that is, an exact sequence in which every $P _ {i}$ is a projective $\mathbf Z G$- module. Then $H ^ { n } ( G, A)$ is the $n$- th cohomology group of the complex

$$0 \rightarrow \mathop{\rm Hom} _ {G} ( P _ {0} , A) \rightarrow ^ { {d _ 0} ^ \prime } \ \mathop{\rm Hom} _ {G} ( P _ {1} , A) \rightarrow \dots ,$$

where $d _ {n} ^ { \prime }$ is induced by $d _ {n}$, that is, $H ^ { n } ( G, A) = \mathop{\rm Ker} d _ {n} ^ { \prime } / \mathop{\rm Im} d _ {n - 1 } ^ { \prime }$.

The homology groups of a group are defined using the dual construction, in which $\mathop{\rm Hom} _ {G}$ is replaced everywhere by $\otimes _ {G}$.

The set of functors $A \mapsto H ^ { n } ( G, A)$, $n = 0, 1 \dots$ is a cohomological functor (see Homology functor; Cohomology functor) on the category of left $G$- modules.

A module of the form $B = \mathop{\rm Hom} ( \mathbf Z [ G], X)$, where $X$ is an Abelian group and $G$ acts on $B$ according to the formula

$$( g \phi ) ( t) = \ \phi ( tg),\ \ \phi \in B,\ \ t \in \mathbf Z G,$$

is said to be co-induced. If $A$ is injective or co-induced, then $H ^ { n } ( G, A) = 0$ for $n \geq 1$. Every module $A$ is isomorphic to a submodule of a co-induced module $B$. The exact homology sequence for the sequence

$$0 \rightarrow A \rightarrow B \rightarrow B/A \rightarrow 0$$

then defines isomorphisms $H ^ { n } ( G, B/A) \simeq H ^ { n + 1 } ( G, A)$, $n \geq 1$, and an exact sequence

$$B ^ {G} \rightarrow \ ( B/A) ^ {G} \rightarrow \ H ^ {1} ( G, A) \rightarrow 0.$$

Therefore, the computation of the $( n + 1)$- dimensional cohomology group of $A$ reduces to calculating the $n$- dimensional cohomology group of $B/A$. This device is called dimension shifting.

Dimension shifting enables one to give an axiomatic definition of cohomology groups, namely, they can be defined as a sequence of functors $A \mapsto H ^ { n } ( G, A)$ from the category of $G$- modules into the category of Abelian groups forming a cohomological functor and satisfying the condition that $H ^ { n } ( G, B) = 0$, $n \geq 1$, for every co-induced module $B$.

The groups $H ^ { n } ( G, A)$ can also be defined as equivalence classes of exact sequences of $G$- modules of the form

$$0 \rightarrow A \rightarrow M _ {1} \rightarrow \dots \rightarrow M _ {n} \rightarrow \mathbf Z \rightarrow 0$$

with respect to a suitably defined equivalence relation (see [1], Chapt. 3, 4).

To compute the cohomology groups, the standard resolution of the trivial $G$- module $\mathbf Z$ is generally used, in which $P _ {n} = \mathbf Z [ G ^ {n + 1 } ]$ and, for $( g _ {0} \dots g _ {n} ) \in G ^ {n + 1 }$,

$$d _ {n} ( g _ {0} \dots g _ {n} ) = \ \sum _ {i = 0 } ^ { n } (- 1) ^ {i} ( g _ {0} \dots \widehat{g} _ {i} \dots g _ {n} ),$$

where the symbol $\widehat{ {}}$ over $g _ {i}$ means that the term $g _ {i}$ is omitted. The cochains in $\mathop{\rm Hom} _ {G} ( P _ {n} , A)$ are the functions $f ( g _ {0} \dots g _ {n} )$ for which $gf ( g _ {0} \dots g _ {n} ) = f ( gg _ {0} \dots gg _ {n} )$. Changing variables according to the rules $g _ {0} = 1$, $g _ {1} = h _ {1}$, $g _ {2} = h _ {1} h _ {2} \dots g _ {n} = h _ {1} \dots h _ {n}$, one can go over to inhomogeneous cochains $f ( h _ {1} \dots h _ {n} )$. The coboundary operation then acts as follows:

$$d ^ \prime f ( h _ {1} \dots h _ {n + 1 } ) = \ h _ {1} f ( h _ {2} \dots h _ {n + 1 } ) +$$

$$+ \sum _ {i = 1 } ^ { n } (- 1) ^ {i} f ( h _ {1} \dots h _ {i} h _ {i + 1 } \dots h _ {n + 1 } ) +$$

$$+ (- 1) ^ {n + 1 } f ( h _ {1} \dots h _ {n} ).$$

For example, a one-dimensional cocycle is a function $f: G \rightarrow A$ for which $f ( g _ {1} g _ {2} ) = g _ {1} f ( g _ {2} ) + f ( g _ {1} )$ for all $g _ {1} , g _ {2} \in G$, and a coboundary is a function of the form $f ( g) = ga - a$ for some $a \in A$. A one-dimensional cocycle is also said to be a crossed homomorphism and a one-dimensional coboundary a trivial crossed homomorphism. When $G$ acts trivially on $A$, crossed homomorphisms are just ordinary homomorphisms and all the trivial crossed homomorphisms are 0, that is, $H ^ {1} ( G, A) = \mathop{\rm Hom} ( G, A)$ in this case.

The elements of $H ^ {1} ( G, A)$ can be interpreted as the $A$- conjugacy classes of sections $G \rightarrow F$ in the exact sequence $1 \rightarrow A \rightarrow F \rightarrow G \rightarrow 1$, where $F$ is the semi-direct product of $G$ and $A$. The elements of $H ^ {2} ( G, A)$ can be interpreted as classes of extensions of $A$ by $G$. Finally, $H ^ {3} ( G, A)$ can be interpreted as obstructions to extensions of non-Abelian groups $H$ with centre $A$ by $G$( see [1]). For $n > 3$, there are no analogous interpretations known (1978) for the groups $H ^ { n } ( G, A)$.

If $H$ is a subgroup of $G$, then restriction of cocycles from $G$ to $H$ defines functorial restriction homomorphisms for all $n$:

$$\mathop{\rm res} : \ H ^ { n } ( G, A) \rightarrow \ H ^ { n } ( H, A).$$

For $n = 0$, $\mathop{\rm res}$ is just the imbedding $A ^ {G} \subset A ^ {H}$. If $G/H$ is some quotient group of $G$, then lifting cocycles from $G/H$ to $G$ induces the functorial inflation homomorphism

$$\inf : \ H ^ { n } ( G/H,\ A ^ {H} ) \rightarrow \ H ^ { n } ( G, A).$$

Let $\phi : G ^ \prime \rightarrow G$ be a homomorphism. Then every $G$- module $A$ can be regarded as a $G ^ \prime$- module by setting $g ^ \prime a = \phi ( g ^ \prime ) a$ for $g ^ \prime \in G ^ \prime$. Combining the mappings $\mathop{\rm res}$ and $\inf$ gives mappings $H ^ { n } ( G ^ \prime , A) \rightarrow H ^ { n } ( G, A)$. In this sense $H ^ {*} ( G, A)$ is a contravariant functor of $G$. If $\Pi$ is a group of automorphisms of $G$, then $H ^ { n } ( G, A)$ can be given the structure of a $\Pi$- module. For example, if $H$ is a normal subgroup of $G$, the groups $H ^ { n } ( H, A)$ can be equipped with a natural $G/H$- module structure. This is possible thanks to the fact that inner automorphisms of $G$ induce the identity mapping on the $H ^ { n } ( G, A)$. In particular, for a normal subgroup $H$ in $G$, $\mathop{\rm Im} \mathop{\rm res} \subset H ^ { n } ( H, A) ^ {G/H}$.

Let $H$ be a subgroup of finite index in the group $G$. Using the norm map $N _ {G/H} : A ^ {H} \rightarrow A ^ {G}$, one can use dimension shifting to define the functorial co-restriction mappings for all $n$:

$$\mathop{\rm cores} : \ H ^ { n } ( H, A) \rightarrow \ H ^ { n } ( G, A).$$

These satisfy $\mathop{\rm cores} \cdot \mathop{\rm res} = ( G: H)$.

If $H$ is a normal subgroup of $G$ then there exists the Lyndon spectral sequence with second term $E _ {2} ^ {p,q} = H ^ { p } ( G/H, H ^ { q } ( H, A))$ converging to the cohomology $H ^ { n } ( G, A)$( see [1], Chapt. 11). In small dimensions it leads to the exact sequence

$$0 \rightarrow H ^ {1} ( G/H, A ^ {H} ) \mathop \rightarrow \limits ^ { \inf } \ H ^ {1} ( G, A) \mathop \rightarrow \limits ^ { { \mathop{\rm res}} } \ H ^ {1} ( H, A) ^ {G/H} \mathop \rightarrow \limits ^ { { \mathop{\rm tr}} }$$

$$\mathop \rightarrow \limits ^ { { \mathop{\rm tr}} } H ^ {2} ( G/H, A ^ {H} ) \mathop \rightarrow \limits ^ { \inf } H ^ {2} ( G, A),$$

where $\mathop{\rm tr}$ is the transgression mapping.

For a finite group $G$, the norm map $N _ {G} : A \rightarrow A$ induces the mapping $\widehat{N} _ {G} : H _ {0} ( G, A) \rightarrow H ^ {0} ( G, A)$, where $H _ {0} ( G, A) = A/J _ {G} A$ and $J _ {G}$ is the ideal of $\mathbf Z G$ generated by the elements of the form $g - 1$, $g \in G$. The mapping $N _ {G}$ can be used to unite the exact cohomology and homology sequences. More exactly, one can define modified cohomology groups (also called Tate cohomology groups) $\widehat{H} {} ^ {n } ( G, A)$ for all $n$. Here

$$\widehat{H} {} ^ {n } ( G, A) = H ^ { n } ( G, A) \ \ \textrm{ for } n \geq 1,$$

$$\widehat{H} {} ^ {n } ( G, A) = H _ {- n - 1 } ( G, A) \ \textrm{ for } n \leq - 1,$$

$$\widehat{H} {} ^ {-} 1 ( G, A) = \mathop{\rm Ker} \widehat{N} _ {G} \ \textrm{ and } \ \widehat{H} _ {0} ( G, A) = \mathop{\rm Coker} \widehat{N} _ {G} .$$

For these cohomology groups there exists an exact cohomology sequence that is infinite in both directions. A $G$- module $A$ is said to be cohomologically trivial if $\widehat{H} {} ^ {n } ( H, A) = 0$ for all $n$ and all subgroups $H \subseteq G$. A module $A$ is cohomologically trivial if and only if there is an $i$ such that $\widehat{H} {} ^ {i} ( H, A) = 0$ and $\widehat{H} {} ^ {i + 1 } ( H, A) = 0$ for every subgroup $H \subseteq G$. Every module $A$ is a submodule or a quotient module of a cohomologically trivial module, and this allows one to use dimension shifting both to raise and to lower the dimension. In particular, dimension shifting enables one to define $\mathop{\rm res}$ and $\mathop{\rm cores}$( but not $\inf$) for all integral $n$. For a finitely-generated $G$- module $A$ the groups $\widehat{H} {} ^ {n } ( G, A)$ are finite.

The groups $\widehat{H} {} ^ {n } ( G, A)$ are annihilated on multiplication by the order of $G$, and the mapping $\widehat{H} ( G, A) \rightarrow \oplus _ {p} \widehat{H} {} ^ {n } ( G _ {p} , A)$, induced by restrictions, is a monomorphism, where now $G _ {p}$ is a Sylow $p$- subgroup (cf. Sylow subgroup) of $G$. A number of problems concerning the cohomology of finite groups can be reduced in this way to the consideration of the cohomology of $p$- groups. The cohomology of cyclic groups has period 2, that is, $\widehat{H} {} ^ {n } ( G, A) \simeq \widehat{H} {} ^ {n + 2 } ( G, A)$ for all $n$.

For arbitrary integers $m$ and $n$ there is defined a mapping

$$\widehat{H} {} ^ {n } ( G, A) \otimes \widehat{H} {} ^ {m} ( G, B) \rightarrow \ \widehat{H} {} ^ {n + m } ( G, A \otimes B),$$

(called $\cup$- product, cup-product), where the tensor product of $A$ and $B$ is viewed as a $G$- module. In the special case where $A$ is a ring and the operations in $G$ are automorphisms, the $\cup$- product turns $\oplus _ {n} \widehat{H} {} ^ {n } ( G, A)$ into a graded ring. The duality theorem for $\cup$- products asserts that, for every divisible Abelian group $C$ and every $G$- module $A$, the $\cup$- product

$$\widehat{H} {} ^ {n } ( G, A) \otimes \widehat{H} {} ^ {- n - 1 } ( G, \mathop{\rm Hom} ( A, C)) \rightarrow \ \widehat{H} {} ^ {-} 1 ( G, C)$$

defines a group isomorphism between $\widehat{H} {} ^ {n } ( G, A)$ and $\mathop{\rm Hom} ( \widehat{H} {} ^ {- n - 1 } ( G, \mathop{\rm Hom} ( A, C)) , \widehat{H} {} ^ {-} 1 ( G, C))$( see [2]). The $\cup$- product is also defined for infinite groups $G$ provided that $n, m > 0$.

Many problems lead to the necessity of considering the cohomology of a topological group $G$ acting continuously on a topological module $A$. In particular, if $G$ is a profinite group (the case nearest to that of finite groups) and $A$ is a discrete Abelian group that is a continuous $G$- module, one can consider the cohomology groups of $G$ with coefficients in $A$, computed in terms of continuous cochains [5]. These groups can also be defined as the limit $\lim\limits _ \rightarrow H ^ { n } ( G/U, A ^ {U} )$ with respect to the inflation mapping, where $U$ runs over all open normal subgroups of $G$. This cohomology has all the usual properties of the cohomology of finite groups. If $G$ is a pro- $p$- group, the dimension over $\mathbf Z /p \mathbf Z$ of the first and second cohomology groups with coefficients in $\mathbf Z /p \mathbf Z$ are interpreted as the minimum number of generators and relations (between these generators) of $G$, respectively.

See [6] for different variants of continuous cohomology, and also for certain other types of cohomology groups. See Non-Abelian cohomology for cohomology with a non-Abelian coefficient group.

References

[1]	S. MacLane, "Homology" , Springer (1963) Zbl 0818.18001 Zbl 0328.18009
[2]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) MR0077480 Zbl 0075.24305
[3]	J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) MR0215665 Zbl 0153.07403
[4]	J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) MR0180551 Zbl 0128.26303
[5]	H. Koch, "Galoissche Theorie der 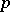-Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970)
[6]	Itogi Nauk. Mat. Algebra. 1964 (1966) pp. 202–235

Comments

The norm map $N _ {G/H} : A ^ {H} \rightarrow A ^ {G}$ is defined as follows. Let $g _ {1} \dots g _ {k}$ be a set of representatives of $G/H$ in $G$. Then $N _ {G/H} ( a) = g _ {1} a + \dots + g _ {k} a$ in $A ^ {G}$. For a definition of the transgression relation in general spectral sequences cf. Spectral sequence; for the particular case of group cohomology, where this gives a relation, sometimes called connection, between $H ^ { n } ( G, A)$ and $H ^ { n + 1 } ( G/H, A ^ {H} )$ for all $n > 0$, cf. also [a1], Chapt. 11, Par. 9.

References

[a1]	K.S. Brown, "Cohomology of groups" , Springer (1982) MR0672956 Zbl 0584.20036