Locally algebraic operator
A linear operator such that for each element of the space under consideration there exists a polynomial in this operator (with scalar coefficients) annihilating this element.
Let 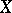 be a linear space over a field
be a linear space over a field 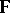 . Let
. Let  be the set of all linear operators with domains and ranges in
be the set of all linear operators with domains and ranges in 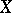 and let
and let
 |
Denote by 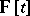 the algebra of all polynomials in the variable
the algebra of all polynomials in the variable 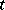 and with coefficients in
and with coefficients in 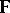 . Usually, in applications it is assumed that the field
. Usually, in applications it is assumed that the field 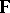 is of characteristic zero and algebraically closed (cf. also Algebraically closed field; Characteristic of a field).
is of characteristic zero and algebraically closed (cf. also Algebraically closed field; Characteristic of a field).
Thus, a linear operator 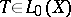 is said to be locally algebraic if for any
is said to be locally algebraic if for any 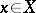 there exists a non-zero polynomial
there exists a non-zero polynomial  such that
such that 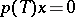 (cf. [a1]). If there exists a non-zero polynomial
(cf. [a1]). If there exists a non-zero polynomial  such that
such that 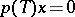 for every
for every 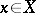 , then
, then 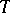 is said to be algebraic (cf. Algebraic operator). Thus, an algebraic operator is locally algebraic, but not conversely.
is said to be algebraic (cf. Algebraic operator). Thus, an algebraic operator is locally algebraic, but not conversely.
A continuous locally algebraic operator acting in a complete linear metric space 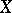 is algebraic (cf. [a4]; for Banach spaces, see [a1]).
is algebraic (cf. [a4]; for Banach spaces, see [a1]).
A locally algebraic operator 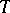 acting in a complete linear metric space
acting in a complete linear metric space 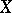 (over the field
(over the field 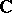 of complex numbers) and that is right invertible (cf. Algebraic analysis) but not invertible, i.e.
of complex numbers) and that is right invertible (cf. Algebraic analysis) but not invertible, i.e.
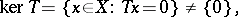 |
is not continuous (cf. [a3]). The assumption about the completeness of  is essential.
is essential.
If  satisfies, for any
satisfies, for any 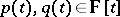 , the conditions:
, the conditions:
i) 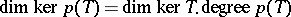 ;
;
ii) 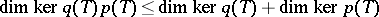 ;
;
iii) 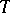 is locally algebraic; then there exists an operator
is locally algebraic; then there exists an operator 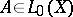 such that
such that
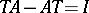 |
(cf. [a2], [a5]). This means that 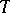 is not an algebraic operator.
is not an algebraic operator.
References
| [a1] | I. Kaplansky, "Infinite Abelian groups" , Univ. Michigan Press (1954) |
| [a2] | J. Mikusiński, "Extension de l'espace linéaire avec dérivation" Studia Math. , 16 (1958) pp. 156–172 |
| [a3] | D. Przeworska-Rolewicz, "Algebraic analysis" , PWN&Reidel (1988) |
| [a4] | D. Przeworska–Rolewicz, S. Rolewicz, "Equations in linear spaces" , PWN (1968) |
| [a5] | R. Sikorski, "On Mikusiński's algebraic theory of differential equations" Studia Math. , 16 (1958) pp. 230–236 |
Locally algebraic operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_algebraic_operator&oldid=50482