Spectral geometry of Riemannian submersions
Let  be a Riemannian submersion. Let
be a Riemannian submersion. Let  and
and  be operators of Laplace type (cf. also Laplace operator) on
be operators of Laplace type (cf. also Laplace operator) on  and
and  on bundles
on bundles  and
and  . Let
. Let  and
and  be the corresponding eigenspaces. Assume given a pull-back
be the corresponding eigenspaces. Assume given a pull-back 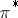 from
from 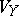 to
to  . One wants to have examples where there exists
. One wants to have examples where there exists
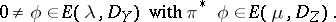 | (a1) |
One also wants to know when
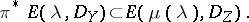 | (a2) |
Let  and let
and let 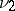 be the volume element on
be the volume element on  . Let
. Let  be the Laplace–Beltrami operator (cf. also Laplace–Beltrami equation). Y. Muto [a8], [a7] observed that
be the Laplace–Beltrami operator (cf. also Laplace–Beltrami equation). Y. Muto [a8], [a7] observed that
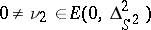 |
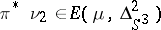 |
for 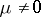 ; he also gave other examples involving principal fibre bundles.
; he also gave other examples involving principal fibre bundles.
S.I. Goldberg and T. Ishihara [a2] and B. Watson [a9] studied this question and determined some conditions to ensure that (a2) holds with  for all
for all 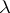 ; this work was later extended in [a5] for the real Laplacian and in [a3] for the complex Laplacian. If (a1) holds for a single eigenvalue, then
; this work was later extended in [a5] for the real Laplacian and in [a3] for the complex Laplacian. If (a1) holds for a single eigenvalue, then 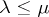 (eigenvalues cannot decrease). See also [a1] for a discussion of the case in which the fibres are totally geodesic. See [a6] for related results in the spin setting. For a survey of the field, see [a4].
(eigenvalues cannot decrease). See also [a1] for a discussion of the case in which the fibres are totally geodesic. See [a6] for related results in the spin setting. For a survey of the field, see [a4].
References
| [a1] | L. Berard Bergery, J.P. Bourguignon, "Laplacians and Riemannian submersions with totally geodesic fibers" Illinois J. Math. , 26 (1982) pp. 181–200 |
| [a2] | S.I. Goldberg, T. Ishihara, "Riemannian submersions commuting with the Laplacian" J. Diff. Geom. , 13 (1978) pp. 139–144 |
| [a3] | P. Gilkey, J. Leahy, J.H. Park, "The eigenforms of the complex Laplacian for a holomorphic Hermitian submersion" Nagoya Math. J. (to appear) |
| [a4] | P. Gilkey, J. Leahy, J.H. Park, "Spinors, spectral geometry, and Riemannian submersions" , Lecture Notes , 40 , Research Inst. Math., Global Analysis Research Center, Seoul Nat. Univ. (1998) |
| [a5] | P. Gilkey, J.H. Park, "Riemannian submersions which preserve the eigenforms of the Laplacian" Illinois J. Math. , 40 (1996) pp. 194–201 |
| [a6] | A. Moroianu, "Opérateur de Dirac et Submersions Riemanniennes" Thesis École Polytechn. Palaiseau (1996) |
| [a7] | Y. Muto, "Riemannian submersion and the Laplace–Beltrami operator" Kodai Math. J. , 1 (1978) pp. 329–338 |
| [a8] | Y. Muto, "Some eigenforms of the Laplace–Beltrami operators in a Riemannian submersion" J. Korean Math. Soc. , 15 (1978) pp. 39–57 |
| [a9] | B. Watson, "Manifold maps commuting with the Laplacian" J. Diff. Geom. , 8 (1973) pp. 85–94 |
| [a10] | Y. Muto, "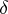 commuting mappings and Betti numbers" Tôhoku Math. J. , 27 (1975) pp. 135–152 commuting mappings and Betti numbers" Tôhoku Math. J. , 27 (1975) pp. 135–152 |
Spectral geometry of Riemannian submersions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_geometry_of_Riemannian_submersions&oldid=50441