Slobodnik property

Recall that a Baire space is a topological space in which every non-empty open subset is of the second category in itself (cf. also Category of a set). A space 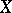is Baire if and only if the intersection of each countable family of dense open sets in 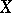is dense (cf. also Dense set).

In what follows, consider a space 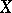equipped with two topologies, 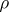and , and assume that is finer than 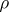. A topology has the Slobodnik property if the intersection of each countable family of -open -dense sets in 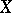is 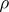-dense. If has the Slobodnik property, then 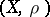is a Baire space. Following a definition of A.R. Todd from [a3], the topologies 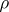and are 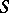-related if for any subset 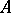of 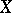, 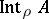(the interior of 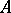with respect to the topology 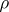) is non-empty if and only if 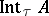is non-empty. 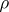If the topologies and are 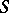-related, then has the Slobodnik property if and only if 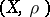is a Baire space, and this is the case if and only if 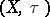is a Baire space.

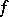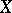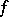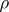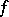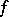Let be a function on of the first Baire class in the topology , i.e. is a pointwise limit of a sequence of -continuous functions (cf. also Baire classes). A very general problem emerges: How large can the set of all -continuity points of be? If has the Slobodnik property, then is 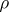-continuous at all points of 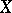except at a set of 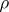-first category. This theorem generalizes Slobodnik's theorem from [a2]: Any limit of a sequence of separately continuous functions on the Euclidean space 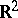is continuous on 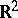, except at a set of the first category. Notice that separately continuous functions are of the first Baire class on 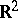, that a function 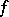is separately continuous on 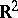exactly when it is continuous in the finer crosswise topology on 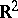(a set 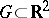is open in this topology if for any 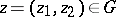there is a 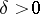such that the "cross"

is a subset of 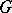), and that the crosswise topology has the Slobodnik property.

A more detailed investigation of the Slobodnik property and related notions can be found in [a1].

References

[a1]	J. Lukeš, J. Malý, L. Zajíček, "Fine topology methods in real analysis and potential theory" , Lecture Notes in Mathematics , 1189 , Springer (1986)
[a2]	S.G. Slobodnik, "Expanding system of linearly closed sets" Mat. Zametki , 19 (1976) pp. 61–84 (In Russian)
[a3]	A.R. Todd, "Quasiregular, pseudocomplete, and Baire spaces" Pacific J. Math. , 95 (1981) pp. 233–250