Weil-Châtelet group
The group of principal homogeneous spaces (cf. Principal homogeneous space) over an Abelian variety. It was shown by A. Weil [1] and, in one special case, by F. Châtelet, that for an arbitrary Abelian variety $ A $
over a field $ k $,
the set $ { \mathop{\rm WC} } ( A, k) $
of principal homogeneous spaces over $ A $,
defined over k, has a group structure. The group $ { \mathop{\rm WC} } ( A, k) $
is isomorphic to the first Galois cohomology group $ H ^ {1} ( k, A) $.
The group $ { \mathop{\rm WC} } ( A, k) $
is always periodic; moreover, if $ k = \mathbf Q $,
it contains elements of arbitrary orders [4], [5]. According to Lang's theorem, $ { \mathop{\rm WC} } ( A, k) = 0 $
if $ k $
is a finite field. The index $ I = { \mathop{\rm ind} } _ {k} ( D) $,
equal to the smallest degree of an extension $ K/k $
for which there exists a $ K $-
rational point $ D $,
is defined for any element $ D \in { \mathop{\rm WC} } ( A, k) $.
If $ { \mathop{\rm dim} } A = 1 $
and $ k $
is an algebraic function field over an algebraically closed field of constants or a local field, $ I $
becomes identical with the order of $ D $
in the group $ { \mathop{\rm WC} } ( A, k) $[6], [10]. In the general case these numbers are different, but $ { \mathop{\rm ord} } ( D) $
is always a divisor of $ I $[7]. The group $ { \mathop{\rm WC} } ( A, k) $
has been computed for local fields $ k $(
see, for instance, [6], [8], [9]).
If $ k $ is a global field, the computation of the group $ { \mathop{\rm WC} } ( A, k) $ is based on the reduction homomorphisms
$$ \phi _ {v} : \mathop{\rm WC} ( A, k ) \rightarrow \mathop{\rm WC} ( A, k _ {v} ), $$
where $ v $ is an arbitrary valuation of $ k $ and $ k _ {v} $ is the completion of $ k $ with respect to $ v $. The kernel $ {\mathop{\amalg\kern-0.30em\amalg}} ( A) $ of the homomorphism
$$ \phi = \sum \phi _ {v} : \mathop{\rm WC} ( A, k) \rightarrow \sum _ { v } \mathop{\rm WC} ( A, k _ {v} ), $$
known as the Tate–Shafarevich group of the Abelian variety $ A $, has been computed only in the case when $ k $ is a field of algebraic functions of one variable over an algebraically closed field of constants [5], [8], [11]. The co-kernel of $ \phi $ has also been described in this case (up to the $ p $- component, where $ p $ is the characteristic of $ k $). The results of these calculations are used in the theory of elliptic surfaces. If $ k $ is an algebraic number field, the structure of the group $ {\mathop{\amalg\kern-0.30em\amalg}} ( A) $ has not been studied to any great extent.
References
| [1] | A. Weil, "On algebraic groups and homogeneous spaces" Amer. J. Math. , 77 (1955) pp. 493–512 MR0074084 Zbl 0065.14202 |
| [2] | M.I. Bashmakov, "Cohomology of Abelian varieties over a number field" Russian Math. Surveys , 27 : 6 (1972) pp. 25–70 Uspekhi Mat. Nauk , 27 : 6 (1972) pp. 25–66 |
| [3] | J. Cassels, "Diophantine equations with special reference to elliptic curves" J. London Math. Soc. , 41 (1966) pp. 193–291 MR0199150 Zbl 0138.27002 |
| [4] | I.R. Shafarevich, "Birational equivalence of elliptic curves" Dokl. Akad. Nauk SSSR , 114 : 2 (1957) pp. 267–270 (In Russian) |
| [5] | I.R. Shafarevich, "Exponents of elliptic curves" Dokl. Akad. Nauk SSSR , 114 : 4 (1957) pp. 714–716 (In Russian) |
| [6] | I.R. Shafarevich, "Principal homogeneous spaces defined over a function field" Trudy Mat. Inst. Steklov. , 64 (1961) pp. 316–346 (In Russian) |
| [7] | S. Lang, J. Tate, "Principal homogeneous spaces over abelian varieties" Amer. J. Math. , 80 (1958) pp. 659–684 MR0106226 Zbl 0097.36203 |
| [8] | A.P. Ogg, "Cohomology of Abelian varieties over function fields" Ann. of Math. (2) , 76 : 2 (1962) pp. 185–212 |
| [9] | J.T. Tate, "WC-groups over 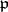 -adic fields" , Sem. Bourbaki , Exp. 156 , Secr. Math. Univ. Paris (1957) -adic fields" , Sem. Bourbaki , Exp. 156 , Secr. Math. Univ. Paris (1957) |
| [10] | S. Lichtenbaum, "The period-index problem for elliptic curves" Amer. J. Math. , 90 : 4 (1968) pp. 1209–1223 |
| [11] | M. Raynaud, "Caractéristique d'Euler–Poincaré d'un faisceau et cohomologie des variétés abéliennes (d'après Ogg–Shafarévitch et Grothendieck)" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 12–30 |
Comments
The Tate–Shafarevich group of certain elliptic curves over number fields has been recently computed ([a1], [a2], [a5]). Also, some new results on the $ p $- component of the Weil–Châtelet groups have been obtained [a3].
References
| [a1] | V.A. Kolyvagin, "Finiteness of 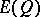 and and 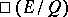 for a class of Weil curves" Math. USSR Izv. , 32 (1989) pp. 523–541 Izv. Akad. Nauk SSSR Ser. Mat. , 52 (1988) pp. 522–540 for a class of Weil curves" Math. USSR Izv. , 32 (1989) pp. 523–541 Izv. Akad. Nauk SSSR Ser. Mat. , 52 (1988) pp. 522–540 |
| [a2] | V.A. Kolyvagin, "On the structure of Shafarevich–Tate groups" S. Block (ed.) et al. (ed.) , Algebraic geometry , Lect. notes in math. , 1479 , Springer (1991) pp. 94–121 MR1181210 Zbl 0753.14025 |
| [a3] | J. Milne, "Arithmetic duality theorems" , Acad. Press (1986) |
| [a4] | J.H. Silverman, "The arithmetic of elliptic curves" , Springer (1986) MR0817210 Zbl 0585.14026 |
| [a5] | K. Rubin, "Tate–Shafarevich groups and 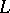 -functions of elliptic curves with complex multiplication" Invert. Math. , 89 (1987) pp. 527–560 MR0903383 -functions of elliptic curves with complex multiplication" Invert. Math. , 89 (1987) pp. 527–560 MR0903383 |
| [a6] | V.A. Kolyvagin, "Euler systems" P. Cartier (ed.) et al. (ed.) , Grothendieck Festschrift , II , Birkhäuser (1990) pp. 435–484 |
| [a7] | K. Rubin, "The work of Kolyvagin on the arithmetic of elliptic curves" W.P. Barth (ed.) et al. (ed.) , Arithmetic of Complex Manifolds , Lect. notes in math. , 1399 , Springer (1989) pp. 128–136 |
Weil-Châtelet group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil-Ch%C3%A2telet_group&oldid=50312