A-operation
operation $ {\mathcal A} $
A set-theoretical operation, discovered by P.S. Aleksandrov [1] (see also [2], [3]). Let $ \{ E _ {n _ {1} \dots n _ {k} } \} $ be a system of sets indexed by all finite sequences of natural numbers. The set
$$ P = \cup _ {n _ {1} \dots n _ {k} , . . } \cap _ { k=1 } ^ \infty E _ {n _ {1} {} \dots n _ {k} } , $$
where the union is over all infinite sequences of natural numbers, is called the result of the $ {\mathcal A} $- operation applied to the system $ \{ E _ {n _ {1} \dots n _ {k} } \} $.
The use of the $ {\mathcal A} $- operation for the system of intervals of the number line gives sets (called $ {\mathcal A} $- sets in honour of Aleksandrov) which need not be Borel sets (see $ {\mathcal A} $- set; Descriptive set theory). The $ {\mathcal A} $- operation is stronger than the operation of countable union and countable intersection, and is idempotent. With respect to $ {\mathcal A} $- operations, the Baire property (of subsets of an arbitrary topological space) and the property of being Lebesgue measurable are invariant.
References
| [1] | P.S. Aleksandrov, C.R. Acad. Sci. Paris , 162 (1916) pp. 323–325 |
| [2] | P.S. Aleksandrov, "Theory of functions of a real variable and the theory of topological spaces" , Moscow (1978) (In Russian) |
| [3] | A.N. Kolmogorov, "P.S. Aleksandrov and the theory of 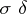 -operations" Uspekhi Mat. Nauk , 21 : 4 (1966) pp. 275–278 (In Russian) -operations" Uspekhi Mat. Nauk , 21 : 4 (1966) pp. 275–278 (In Russian) |
| [4] | M.Ya. Suslin, C.R. Acad. Sci. Paris , 164 (1917) pp. 88–91 |
| [5] | N.N. Luzin, , Collected works , 2 , Moscow (1958) pp. 284 (In Russian) |
| [6] | K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) (Translated from French) |
Comments
The $ {\mathcal A} $- operation is in the West usually attributed to M.Ya. Suslin [4], and is therefore also called the Suslin operation, the Suslin $ {\mathcal A} $- operation or the Suslin operation $ {\mathcal A} $. $ {\mathcal A} $- sets are usually called analytic sets.
A-operation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=A-operation&oldid=50301