Weierstrass representation of a minimal surface
Let 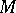 be a Riemann surface. A harmonic conformal mapping
be a Riemann surface. A harmonic conformal mapping 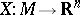 then defines a minimal surface in
then defines a minimal surface in 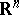 ,
, 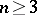 (cf. also Harmonic function; Conformal mapping). Let
(cf. also Harmonic function; Conformal mapping). Let 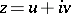 be local isothermal coordinates; then
be local isothermal coordinates; then
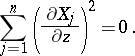 |
Since 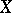 is harmonic,
is harmonic,
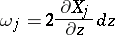 |
is a holomorphic 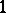 -form on
-form on 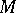 . Hence any (branched) minimal surface in
. Hence any (branched) minimal surface in 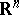 can be given by
can be given by  meromorphic
meromorphic 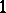 -forms
-forms 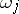 satisfying
satisfying 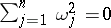 , and
, and 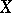 can be expressed as
can be expressed as
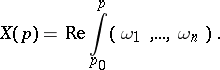 | (a1) |
Such an 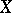 is well defined on
is well defined on 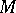 if and only if for any loop
if and only if for any loop 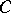 in
in 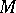 ,
,
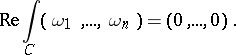 | (a2) |
For 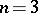 , one gets a meromorphic function
, one gets a meromorphic function 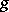 and a meromorphic
and a meromorphic 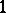 -form
-form 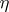 ,
,
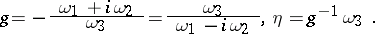 |
On the other hand, given a meromorphic function 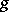 and a meromorphic
and a meromorphic 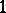 -form
-form 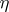 on
on 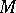 , define
, define
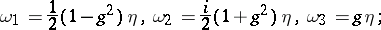 | (a3) |
then 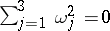 . Thus, (a3) together with (a1) defines a minimal surface in
. Thus, (a3) together with (a1) defines a minimal surface in 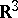 and is called the Weierstrass representation of the minimal surface via the Weierstrass data
and is called the Weierstrass representation of the minimal surface via the Weierstrass data 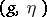 .
.
The meromorphic function 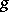 has the geometric meaning that it is the composite of the spherical mapping (or unit normal vector)
has the geometric meaning that it is the composite of the spherical mapping (or unit normal vector) 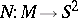 and the stereographic projection from the north pole, where
and the stereographic projection from the north pole, where
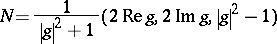 |
and 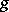 is also called the Gauss map of the minimal surface.
is also called the Gauss map of the minimal surface.
The first fundamental form and the Gaussian curvature of the surface 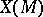 can be expressed via
can be expressed via 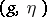 ,
,
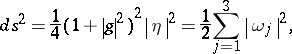 |
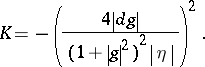 |
Hence 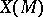 is a regular surface if and only if
is a regular surface if and only if 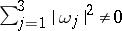 on
on 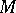 .
.
The second fundamental form of 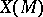 can be expressed as
can be expressed as
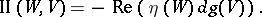 |
Moreover, 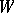 is an asymptotic direction if and only if
is an asymptotic direction if and only if 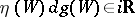 , and
, and 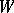 is a principal curvature direction if and only if
is a principal curvature direction if and only if 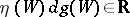 .
.
The local Weierstrass representation was discovered in the 1860{}s by K. Enneper and K. Weierstrass. R. Osserman gave the general form on a Riemann surface in the 1960{}s, see [a1] for more details.
References
| [a1] | R. Osserman., "A survey of minimal surfaces" , Dover (1986) |
Weierstrass representation of a minimal surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_representation_of_a_minimal_surface&oldid=50216