Trace on a C*-algebra

$ A $

An additive functional $ f $ on the set $ A ^ {+} $ of positive elements of $ A $ that takes values in $ [ 0, + \infty ] $, is homogeneous with respect to multiplication by positive numbers and satisfies the condition $ f ( xx ^ {*} ) = f ( x ^ {*} x) $ for all $ x \in A $. A trace $ f $ is said to be finite if $ f ( x) < + \infty $ for all $ x \in A ^ {+} $, and semi-finite if $ f ( x) = \sup \{ {f ( y) } : {y \in A, y \leq x, f( y) < + \infty } \} $ for all $ x \in A ^ {+} $. The finite traces on $ A $ are the restrictions to $ A ^ {+} $ of those positive linear functionals $ \phi $ on $ A $ such that $ \phi ( xy) = \phi ( yx) $ for all $ x, y \in A $. Let $ f $ be a trace on $ A $, let $ \mathfrak N _ {f} $ be the set of elements $ x \in A $ such that $ f ( xx ^ {*} ) < + \infty $, and let $ \mathfrak M _ {f} $ be the set of linear combinations of products of pairs of elements of $ \mathfrak N _ {f} $. Then $ \mathfrak N _ {f} $ and $ \mathfrak M _ {f} $ are self-adjoint two-sided ideals of $ A $, and there is a unique linear functional $ \phi $ on $ \mathfrak M _ {f} $ that coincides with $ f $ on $ \mathfrak M _ {f} \cap A ^ {+} $. Let $ f $ be a lower semi-continuous semi-finite trace on a $ C ^ {*} $- algebra $ A $. Then the formula $ s ( x, y) = \phi ( y ^ {*} x) $ defines a Hermitian form on $ \mathfrak N _ {f} $, with respect to which the mapping $ \lambda _ {f} ( x): x \mapsto xy $ of $ \mathfrak N _ {f} $ into itself is continuous for any $ x \in A $. Put $ N _ {f} = \{ {x \in \mathfrak N _ {f} } : {s ( x, x) = 0 } \} $, and let $ H _ {f} $ be the completion of the quotient space $ \mathfrak N _ {f} /N _ {f} $ with respect to the scalar product defined by the form $ s $. By passing to the quotient space and subsequent completion, the operators $ \lambda _ {f} ( x) $ determine certain operators $ \pi _ {f} ( x) $ on the Hilbert space $ H _ {f} $, and the mapping $ x \mapsto \pi _ {f} ( x) $ is a representation of the $ C ^ {*} $- algebra $ A $ in $ H _ {f} $. The mapping $ f \mapsto \pi _ {f} $ establishes a one-to-one correspondence between the set of lower semi-continuous semi-finite traces on $ A $ and the set of representations of $ A $ with a trace, defined up to quasi-equivalence.

References

[1]	J. Dixmier, "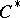 algebras" , North-Holland (1977) (Translated from French)

Comments

Cf. also $ C ^ {*} $- algebra; Trace; Quasi-equivalent representations.

References

[a1]	O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979)