Synthesis problems
An aggregate of problems centered on the problem of constructing a control system with a prescribed way of functioning. A control system is usually made up of elements which are themselves simple control systems. Formerly synthesis meant that the structure of the elements, a rule for combining them and a means of using the structure of the control system to define the function which it realizes are given.
Every class of control systems gives rise in a natural way to a specific class of functions. A synthesis problem originally consisted of constructing a control system realizing a given function from this class.
Examples. 1) Given a Boolean function, construct a formula which realizes it. 2) Given a set of Boolean functions, construct a multipolar contact scheme which realizes this set. 3) Given an exact description of the behaviour of an automaton, construct the automaton itself. 4) Given a computable function, find an algorithm that computes it, or compose the corresponding program.
The above examples are concerned with discrete mathematics. However, the following are characteristic examples of a continuous nature. a) Given the logarithmic amplitude-frequency characteristic of an (automatic) control system (or, more generally, working conditions of it such as perturbation and control actions, disturbances, restrictions on working time, etc.), synthesize an (automatic) control system with these characteristics. b) Given a system of linear equations and inequalities, and also a linear function, construct a computing scheme which maximizes this function on the solution set of this system. c) Given a system of differential equations and a desired degree of accuracy for its solution, find an algorithm for solving this system numerically to within this degree of accuracy.
It is conventional to treat the last three examples as belonging to continuous mathematics, although the search for an approximate numerical solution already presupposes the approximation of continuous functions by discrete ones. These problems thus involve an interplay between continuous and discrete mathematics.
The mathematical formulation of synthesis problems presupposes an exact indication of the language in which a function is given. Which problems can arise in the solution of synthesis problems depend on this language. In the majority of cases there is a comparatively simple method for constructing a control system of a canonical form.
However, when the class of control systems is not too small, the problem can have many other solutions; the problem naturally arises of choosing one that is optimal in some sense. To this end one introduces a functional characterizing the quality of a control system, such as the number of elements in it, its cost, its volume, its capacity (that is, the greatest number of its elements in an active state), its working time, the probability of breakdown, etc. It is important that this functional, usually called the complexity, should accurately reflect the property required of the control system, and be readily computable from it. A refinement of synthesis problems consists of constructing, for a given function, a control system that realizes it with minimal complexity.
In fact, such a definite formulation of the problem is only possible for finite models of control systems. As a result, all synthesis problems are more clearly stated in this case, and so finite models are given most attention below.
For finite models of control systems a typical situation is that in which the problem has a trivial solution. For example, if one wishes to minimize the number of elements in a scheme, then the trivial method of solution consists in first listing all schemes containing one element and verifying whether or not one of them realizes the given function, then listing all schemes containing two elements and verifying again, etc. until one finds a scheme that realizes the given function. This scheme then has the minimum number of elements.
However, due to the large number of steps required, the trivial method is not very effective. Besides, if the complexity of the function to be realized exceeds a certain comparatively low threshold, then the trivial method becomes practically unworkable and the use of the fastest computers extends its scope only slightly. This means that a further refinement of the formulation of synthesis problems is required.
The tendencies listed here are illustrated below for the example of one class of control systems, diagrams of functional elements (cf. Diagram of functional elements), for the special case where complexity is taken to be the number of elements in the scheme. The functions realizable by this type of control system are those of the algebra of logic (Boolean functions).
First of all, one must note that the non-applicability of solving by the trivial method is only one of the reasons leading to a revision of the formulation of synthesis problems. There is a conjecture that any algorithm which constructs for every Boolean function a scheme with a minimal number of elements inevitably contains in some sense a listing of all Boolean functions. As positive evidence for this there is a theorem which states that if one considers an infinite set of Boolean functions containing one most complex function for every number of variables, and if one takes the closure of this set under the operations of renaming variables (without identification) and substituting constants, then one obtains the set consisting of all general Boolean functions (up to inessential variable functions). This conjecture has much indirect support confirming the fact that even if one relaxes the requirement on the number of elements that are allowed for the construction of the schemes close to optimal, but retains the requirement that the algorithm be applicable to every Boolean function, then the listing cannot be reduced. The concept of the inevitability in principle of listing is another basic reason for modifying the formulation of synthesis problems. There are several possibilities here.
The Shannon approach (named after C.E. Shannon, who first suggested it for contact schemes) is connected with the function
$$ L ( n) = \max L ( f ), $$
where $ L ( f ) $ is the smallest possible number of elements in a scheme realizing a function $ f $, and the maximum is taken over all Boolean functions $ f $ in $ n $ variables. $ L ( f ) $ and $ L ( n) $ depend on the basis, that is, on the set of function elements that can be used in the construction of the schemes. Synthesis problems consist of finding an effective method of constructing, for any Boolean function in $ n $ variables, schemes with a number of elements essentially not greater than $ L ( n) $.
For a more general formulation of the problem, one assigns to every functional element $ E $ a positive number $ L ( E) $ as the complexity of this element, which depends only on the function realizable by the element $ E $, and ascribes to every scheme $ S $ the complexity
$$ L ( S) = \ \sum L ( E), $$
where the summation is over all the elements of the scheme $ S $. For every Boolean function $ f $ the complexity of its realization (in a given basis) is defined as follows:
$$ L ( f ) = \ \min L ( S) $$
where the minimum is taken over all schemes $ S $ realizing $ f $. Then, as before, one sets $ L ( n) = \max L ( f ) $, and for an arbitrary Boolean function in $ n $ variables it is required to construct a scheme of complexity not greater (or not much greater) than $ L ( n) $.
For this approach one needs to be able to compute $ L ( n) $ or bound it accurately, at least from below. It turns out that one can obtain a fairly good lower bound for $ L ( n) $ by the power method, which is based on the following consideration. The number of all possible schemes realizing Boolean functions in $ n $ variables and having complexity not greater than $ L ( n) $, cannot be smaller than the total number of Boolean functions in $ n $ variables. In the power method, one needs only obtain a satisfactory upper bound for the number of schemes under consideration.
One can then judge to a great extent the quality of an arbitrary universal synthesis method (that is, a method suitable for any Boolean function) by how many times the complexity of the schemes constructed by it for a given $ n $ differs from the lower bound for $ L ( n) $. At the same time, the complexity of these schemes serves as a constructive bound for $ L ( n) $ and is asymptotically equal to it as $ n \rightarrow \infty $. Thus, this is asymptotically the best synthesis method and enables one to describe the asymptotic behaviour of $ L ( n) $. Let
$$ \rho = \min \ \frac{L ( E) }{i - 1 } , $$
where $ i $ is the number of occurrences of an element $ E $ and the minimum is taken over all $ E $ for which $ i \geq 2 $. Then
$$ L ( n) \sim \rho { \frac{2 ^ {n} }{n} } . $$
For other classes of control systems, $ L ( S) $, and also the complexities $ L ( f ) $ and $ L ( n) $, are defined in a similar way. For a contact scheme $ S $, $ L ( S) $ is usually the number of contacts in it, and when $ S $ is a formula, it is the number of symbols denoting variables in it. For automata and Turing machines (cf. Turing machine), $ L ( S) $ is sometimes taken to be the number of states. In these cases the corresponding asymptotic behaviour of $ L ( n) $
is shown in Table 1.
<tbody> </tbody>
|
For other types of complexity, such as the probability of error, and for other classes of control systems, such as automata, the corresponding asymptotic relation may contain not one but two or more parameters, and, in general, the problem of finding asymptotics (say for automata) is algorithmically unsolvable.
An analysis of the lower bound for $ L ( n) $ shows that, in fact, for almost-all Boolean functions in $ n $ variables, the complexity of realization is asymptotically not less than $ L ( n) $. This means that a given synthesis method for almost-all Boolean functions yields almost the simplest schemes.
However, first, despite the fact that the class contains almost-all Boolean functions, for sufficiently large $ n $ none of the functions in the class can be clearly described, and secondly, it consists of the hardest functions to realize, and these are seldom encountered in problems of an applied nature. So, such functions are not of great interest, and it again becomes necessary to modify the formulation of the synthesis problem.
It must be noted that functions for which the synthesis problem is actually important form a negligible part of all Boolean functions, and if the conjecture on the necessity of listing is true as stated, any effective universal synthesis method will automatically give in some cases schemes that are by no means the simplest. It is impossible to describe the set of these functions, and the problem arises of classifying Boolean functions for synthesis purposes. This approach to the formulation of the problem is concerned with the selection of important classes of functions, with the creation of special synthesis methods for them, each oriented towards a function of a specific class, and also with estimating the quality of the schemes thus obtained.
An effective means for solving such problems is provided by the local coding principle. This principle presupposes a coding of the functions in the class under consideration in such a way that the value of a function can be computed using a comparatively small part of the code. If one succeeds in realizing certain auxiliary operators in a sufficiently simple way, then the local coding principle gives a synthesis method which is asymptotically optimal for the class considered. Moreover, the following relation holds with a fair degree of generality:
$$ L ( N _ {n} ) \sim \rho \frac{ \mathop{\rm log} _ {2} | N _ {n} | }{ \mathop{\rm log} _ {2} \mathop{\rm log} _ {2} | N _ {n} | } , $$
where $ N _ {n} $ is the subset of those functions of the class that depend on a given set of $ n $ variables, and
$$ L ( N _ {n} ) = \ \max L ( f ), $$
where the maximum is taken over all Boolean functions $ f $ in $ N _ {n} $( $ \rho = 1 $ here).
The concrete form taken by this asymptotic relation is most conveniently illustrated on classes of Boolean functions which take the value 1 at a given number of points. The most typical examples are shown in Table 2.
<tbody> </tbody>
|
On the basis of the local coding principle good synthesis methods have also been obtained for very narrow classes of functions (such as symmetric functions), i.e. for those functions which are of most interest from a practical point of view. However, in the case under consideration, the lower bound obtained by the power method turns out to be too weak for judging the quality of schemes. As far as restricting the class of functions being considered at a given time is concerned, this is inevitable, since the limiting case of a narrow class is one containing not more than one function in each number of variables. This means in practice that one considers individual concrete functions.
Two problems arise here. $ \alpha $) To construct, for a given concrete function $ f $, a scheme with the smallest possible number of elements, and thus to obtain an upper bound for $ L ( f ) $. $ \beta $) To obtain the best possible lower bound for $ L ( f ) $. Of these problems, the first is usually the simpler, since for its solution it is sufficient in the final analysis to construct just one scheme, whereas the second requires a survey in some sense of all the schemes realizing $ f $. This motivated a whole new trend in the search for methods of obtaining lower bounds for concrete functions.
In finding lower bounds that are linear in $ n $, the number of arguments of the function (or, in general, the volume of input information) usually causes no great difficulties. Finding stricter lower bounds is a significantly more complex problem. The first examples of this type were a lower bound of order $ n ^ {1.5} $ for formulas in the basis $ \{ \&, \lor , \overline{ {}}\; \} $ realizing a linear function (with addition modulo 2) of $ n $ arguments, and a lower bound of order $ n ^ {2} / \mathop{\rm log} _ {2} ^ {2} n $ for Markov normal algorithms (cf. Normal algorithm) applied to words of length $ n $. The best lower bounds so far (1984) obtained are of order $ n ^ {2} $, provided one ignores those obtained under very strong restrictions on the class of control systems (for example, when the system of elements is incomplete) or by the use of powerful means for representing a function that actually include a listing all functions.
The non-triviality of the investigation into the complexity of realizing concrete functions is also indicated by the fact that many problems (such as the multiplication of integers, the multiplication of matrices, and the recognition of symmetry of a word on multi-tape Turing machines) for which comparatively high lower bounds were expected, turned out to be in actual fact simpler than at first supposed.
In minimizing other parameters of schemes, such as delays, probability of a breakdown, etc. roughly the same problems arise. One can establish a definite connection between various parameters, and thanks to the simulation of certain objects by others, this can often be done for parameters of control systems in different classes. Thus, results obtained in synthesis problems are not isolated, but are closely interrelated, and can often be transferred from one domain into another.
Much of the above carries over to infinite models of control systems. However, in the formulation of synthesis problems, and even more so in their solution, the situation is significantly more complex.
References
| [1] | O.B. Lupanov, "On a certain approach to the synthesis of control systems - the local coding principle" Probl. Kibernet. , 14 (1965) pp. 31–110 (In Russian) |
| [2] | S.V. Yablonskii, "On algorithmic difficulties in designing minimal control circuits" Probl. Kibernet. , 2 (1959) pp. 75–121 (In Russian) |
Comments
Given a discrete- or continuous-time input-output dynamical system or control dynamical system, also simply called dynamical system,
$$ x( t+ 1) = f( x( t), u( t), t) ,\ \ \dot{x} = f( x, u , t) , $$
$$ x \in \mathbf R ^ {n} ,\ u \in \mathbf R ^ {m} , $$
$$ y( t) = h( x( t)) ,\ y = h( x) , $$
$$ y \in \mathbf R ^ {p} , $$
and a starting point $ x( 0) \in \mathbf R ^ {n} $ at time zero, the system $ \Sigma $ defines a function $ b( \Sigma ) $ from a space of input functions $ {\mathcal U} $ to a space of output function $ {\mathcal J} $, sometimes called the behaviour of the initialized system $ ( \Sigma , x( 0)) $. Given a behaviour $ b $, one now has the synthesis problem of finding a dynamical system $ \Sigma $( of a suitable class) such that $ b( \Sigma ) = b $. One says then that $ \Sigma $ realizes $ b $, and in this setting the synthesis problem is usually called the realization problem and one speaks of realization theory.
In the case of a time-invariant linear dynamical input-output system
$$ \dot{x} = Ax+ Bu ,\ \ y = Cx, $$
$$ A \in \mathbf R ^ {n \times n } ,\ A \in \mathbf R ^ {m \times m } ,\ C \in \mathbf R ^ {p \times n } $$
(or its discrete counterpart), its behaviour is completely determined by its transfer function
$$ T( s) = C( sI- A) ^ {-} 1 B = \ s ^ {-} 1 T _ {0} + s ^ {-} 2 T _ {1} + s ^ {-} 3 T _ {2} + \dots , $$
with
$$ T _ {i} = CA ^ {i} B, $$
which gives the Laplace transforms (or $ z $- transforms in the discrete-time case) of the input and output functions. In this case one speaks of realizing the strictly proper rational matrix function $ T( s) $ or of the series of Markov parameters $ T _ {0} , T _ {1} ,\dots $. Thus, a realization of $ T _ {0} , T _ {1} \dots $ is a triple of matrices $ A , B , C $ such that $ T _ {i} = CA ^ {i} B $, $ i = 0, 1,\dots $. The least $ n $ such that there exists a realization with $ A $ an $ ( n \times n) $- matrix is the McMillan degree of $ ( T _ {0} , T _ {1} , . . . ) $ or $ T( s) $. It is equal to the rank of the infinite block Hankel matrix
$$ \left (
If one is looking for $ A , B , C $ such that $ T _ {i} = CA ^ {i} B $, $ i = 0 \dots k $, one speaks of a partial realization problem.
There are realization algorithms that are locally continuous in the parameters $ T _ {0} , T _ {1} , . . . $. There exists a global continuous realization if and only if $ p = 1 $( one output) or $ m = 1 $( one input). (Non-existence of continuous canonical forms.)
Realizations of matrix functions and, more generally, operator-valued functions have proved to be a valuable tool in, e.g., minimal factorization and Wiener–Hopf factorization of matrix and operator-valued functions, cf. e.g. [a11]–[a13].
Analogous realization questions arise for stochastic dynamical systems; cf. e.g. [a5] and [a6] for a discussion of two stochastic realization problems (state space models for Gaussian random processes, transmission line models realizing a given covariance function).
For a survey of non-linear deterministic finite-dimensional realization theory, cf. e.g. [a10].
In control theory the phrase "synthesis problem in control theorysynthesis problem" mostly refers to the problem of finding for a given input-output dynamical system $ \Sigma $ a suitable feedback law $ v = k( z) $, where $ z $ is some (measured) output. (Or, more generally, a dynamical input-output system with input $ z $ and output $ v $ such that the resulting closed-loop system System Controller $ u $ $ z $ $ v $ $ y $
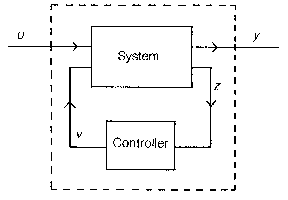
Figure: s091910a
has some desired behaviour. For instance, that certain disturbances are suppressed or that $ u \mapsto y $ matches a pre-given behaviour.)
For the specific question of the synthesis or realization of electrical networks, cf. (the editorial comments to) Network and the references given there.
References
| [a1] | N. Pippenger, "The complexity of monotone Boolean functions" Math. Syst. Theory , 11 (1978) pp. 289–316 |
| [a2] | A.A. Razborov, "Lower bounds for the monotone complexity of some Boolean functions" Soviet Math. Dokl. , 31 (1985) pp. 354–357 Dokl. Akad. Nauk SSSR , 281 : 4 (1985) pp. 798–801 |
| [a3] | J.E. Savage, "The complexity of computing" , Wiley (1976) |
| [a4] | I. Wegener, "The complexity of Boolean functions" , Wiley & Teubner (1987) |
| [a5] | A. Lindquist, G. Picci, "State space models for Gaussian stochastic processes" M. Hazewinkel (ed.) J.C. Willems (ed.) , Stochastic Systems: Math. of Filtering and Identification and Appl. , Reidel (1981) pp. 169–204 |
| [a6] | P. DeWilde, J.T. Fokkema, I Widya, "Inverse scattering and linear prediction" M. Hazewinkel (ed.) J.C. Willems (ed.) , Stochastic Systems: Math. of Filtering and Identification and Appl. , Reidel (1981) pp. 307–350 |
| [a7] | M. Hazewinkel, "(Fine) moduli spaces for linear systems: what are they and what are they good for" C.I. Byrnes (ed.) C.F. Martin (ed.) , Geometrical Methods for the Theory of Linear Systems , Reidel (1980) pp. 125–193 |
| [a8] | A.H. Zemanian, "Realizability theory for continuous linear systems" , Acad. Press (1972) |
| [a9] | R.E. Kalman, P.L. Falb, M.A. Arbib, "Topics in mathematical systems theory" , McGraw-Hill (1969) |
| [a10] | B. Jakubczyk, "Realization theory for nonlinear systems: three approaches" M. Fliess (ed.) M. Hazewinkel (ed.) , Algebraic and geometric methods in nonlinear control theory , Reidel (1986) pp. 3–32 |
| [a11] | H. Bart, I. Gohberg, M.A. Kaashoek, "Minimal factorization of matrix and operation functions" , Birkhäuser (1979) |
| [a12] | K. Clancey, I. Gohberg, "Factorization of matrix functions and singular integral operators" , Birkhäuser (1981) |
| [a13] | H. Bart, I. Gohberg, M.A. Kaashoek, "Explicit Wiener–Hopf bifurcation and realization" I. Gohberg (ed.) M.A. Kaashoek (ed.) , Constructive Methods of Wiener–Hopf Factorization , Birkhäuser (1986) pp. 235–316 |
| [a14] | W.M. Wonham, "Linear multivariable control" , Springer (1974) |
| [a15] | E.D. Sontag, "Mathematical control theory" , Springer (1990) |
Synthesis problems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Synthesis_problems&oldid=49465