Papperitz equation
An ordinary second-order Fuchsian linear differential equation having precisely three singular points:
$$ \tag{1 } w ^ {\prime\prime } + \left ( \frac{1 - \alpha - \alpha ^ \prime }{z-} a + \frac{1 - \beta - \beta ^ \prime }{z-} b + \frac{1- \gamma - \gamma ^ \prime }{z-} c \right ) w ^ \prime + $$
$$ + \left [ \frac{\alpha \alpha ^ \prime ( a- b)( a- c) }{z-} a + \frac{\beta \beta ^ \prime ( b- c)( b- a) }{z-} b\right . + $$
$$ + \left . \frac{\gamma \gamma ^ \prime ( c- a)( c- b) }{z-} c \right ] \frac{w}{(} z- a)( z- b)( z- c) = 0 , $$
$$ \alpha + \alpha ^ \prime + \beta + \beta ^ \prime + \gamma + \gamma ^ \prime = 1; $$
here $ a, b, c $ are pairwise distinct complex numbers, $ \alpha , \alpha ^ \prime $( $ \beta , \beta ^ \prime $ and $ \gamma , \gamma ^ \prime $) are the characteristic exponents at the singular point $ z= a $( respectively, $ z= b $ and $ z= c $). A Papperitz equation is uniquely determined by the assignment of the singular points and the characteristic exponents. In solving a Papperitz equation (1), use is made of Riemann's notation:
$$ w = P \left \{ B. Riemann investigated [[#References|[1]]] the problem of finding all many-valued functions $ w( z) $, analytic in the extended complex plane, which have the following properties: a) the function $ w( z) $ has precisely three singular points $ a, b, c $; b) any three of its branches are connected by a linear equation $$ A _ {1} w _ {1} ( z) + A _ {2} w _ {2} ( z) + A _ {3} w _ {3} ( z) = 0 $$ with constant coefficients; c) the function $ w( z) $ has the simplest singularities at the points $ a, b, c $; namely, in a neighbourhood of the point $ z= a $ there are two branches $ \widetilde{w} _ {1} ( z) $ and $ \widetilde{w} _ {2} ( z) $ satisfying $$ \widetilde{w} _ {1} ( z) = \ ( z- a) ^ \alpha \phi _ {1} ( z) ,\ \ \widetilde{w} _ {2} ( z) = \ ( z- a) ^ {\alpha ^ \prime } \phi _ {2} ( z) , $$ where $ \phi _ {j} ( z) $ $ ( j = 1, 2) $ is holomorphic at $ z= a $; and analogously for $ b $ and $ c $. Riemann, under certain additional assumptions on the numbers $ \alpha , \alpha ^ \prime \dots \gamma ^ \prime $, showed that all such functions can be expressed in terms of hypergeometric functions and that $ w( z) $ satisfies a linear second-order differential equation with rational coefficients, but did not write this equation out explicitly (see [[#References|[1]]]). The equation in question, (1), was given by E. Papperitz [[#References|[2]]]. It is also called the Riemann $ P $- equation, the Riemann equation in Papperitz's form and the Riemann equation, and its solutions are called $ P $- functions. The basic properties of the solutions of a Papperitz equation are as follows. 1) A Papperitz equation is invariant under rational-linear transformations: If $ z _ {1} = ( Az + b)/( Cz + D) $ maps the points $ a, b, c $ to points $ a _ {1} , b _ {1} , c _ {1} $, then $$ P \left \{
2) The transformation
$$ \left ( z- \frac{a}{z-} b \right ) ^ {k} \left ( z- \frac{c}{z-} b \right ) ^ {l} w = \widetilde{w} $$
transforms a Papperitz equation into a Papperitz equation with the same singular points, but with different characteristic exponents:
$$ \left ( z- \frac{a}{z-} b \right ) ^ {k} \left ( z- \frac{c}{z-} b \right ) ^ {l} P \left \{ $$ = \ P \left \{
3) The hypergeometric equation
$$ z( 1- z) w ^ {\prime\prime} + [ C - ( A+ B+ 1) z] w ^ \prime - ABw = 0 $$
is a special case of a Papperitz equation and it corresponds in Riemann's notation to
$$ P \left \{ 4) Each solution of a Papperitz equation can be expressed in terms of the hypergeometric function, $$ \tag{2 } w( z) = \left ( z- \frac{a}{z-}
b \right ) ^ \alpha \left ( z-
\frac{c}{z-}
b \right ) ^ \gamma \times
$$ $$ \times F \left \{ \alpha + \beta + \gamma ; \alpha + \beta
^ \prime + \gamma ; 1 + \alpha -
\alpha ^ \prime ; \frac{( z- a)( c- b) }{( z- b)( c- a) }
\right \}
$$
under the assumption that $ \alpha - \alpha ^ \prime $ is not a negative integer. If none of the differences $ \alpha - \alpha ^ \prime $, $ \beta - \beta ^ \prime $, $ \gamma - \gamma ^ \prime $ are integers, then interchanging in (2) the positions of $ \alpha $ and $ \alpha ^ \prime $ or of $ \gamma $ and $ \gamma ^ \prime $, four solutions of a Papperitz equation are obtained. In addition a Papperitz equation remains unchanged if the positions of the triples $ ( \alpha , \alpha ^ \prime , a) $, $ ( \beta , \beta ^ \prime , b) $, $ ( \gamma , \gamma ^ \prime , c) $ are rearranged; all these rearrangements provide 24 special solutions of a Papperitz equation (1), which were first obtained by E.E. Kummer [5].
References
| [1] | B. Riemann, "Beiträge zur Theorie der durch Gauss'sche Reihe 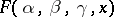 darstellbare Functionen" , Gesammelte math. Werke , Dover, reprint (1953) pp. 67–85 darstellbare Functionen" , Gesammelte math. Werke , Dover, reprint (1953) pp. 67–85 |
| [2] | E. Papperitz, "Ueber verwandte  -Functionen" Math. Ann. , 25 (1885) pp. 212–221 MR1510304 -Functionen" Math. Ann. , 25 (1885) pp. 212–221 MR1510304 |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 MR1424469 MR0595076 MR0178117 MR1519757 Zbl 0951.30002 Zbl 0108.26903 Zbl 0105.26901 Zbl 53.0180.04 Zbl 47.0190.17 Zbl 45.0433.02 Zbl 33.0390.01 |
| [4] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) MR0100119 |
| [5] | E.E. Kummer, "Ueber die hypergeometrische Reihe  " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 |
Papperitz equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Papperitz_equation&oldid=49352