Word metric

length metric

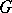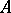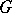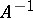A metric on a finitely-generated group , defined as follows. Let be a finite set of generators for . Let be the set of inverses of elements in 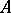. If 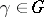is not the identity element, then the length of 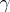is defined as the minimal number of elements of 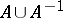, counted with multiplicity, such that 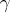can be written as a product of these elements. The length of the identity element is defined to be zero. 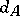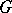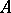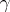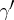The word metric on with respect to is then defined by the following formula: for all and in 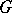, 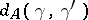is equal to the length of the product 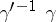. The action of 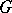by left translations on the metric space 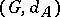is an action by isometries. If 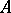and 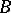are two finite generating sets for 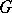, then the identity mapping between the metric spaces 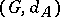and 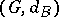is a quasi-isometry.

An equivalent definition is the following: 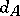is the maximal metric on 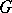that is invariant by the left-action of 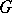on itself, and such that the distance of any element of 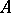or 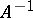to the identity element of 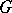is equal to .

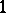The notion of word metric lies at the foundation of geometric group theory. A group 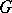(equipped with a finite generating set 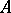) can be canonically imbedded, as the set of vertices, in the associated Cayley graph, which is a simplicial graph. This graph has a canonical metric, and the metric induced on the vertices is the word metric.

The word metric on a group has much to do with the growth function of a finitely-generated group (cf. also Polynomial and exponential growth in groups and algebras; [a1], [a2]; see also [a3], especially Sect. 37, for other and related techniques in the study of groups).

Using the word metric (or the length of words), one defines

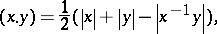where 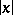is the length of the element .

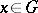A group 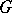is hyperbolic (cf. also Hyperbolic group) if there is a constant 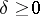such that for all ,

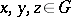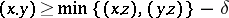(cf. also [a1], [a4]). Hyperbolic groups are always finitely presented (cf. also Finitely-presented group), and as such realizable as the fundamental group of a smooth bounded region 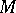. Hyperbolicity is then equivalent to the purely geometric property that there is a constant such that for every smooth closed curve 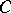in 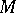, contractible in 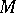and bounding a disc 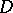, one has

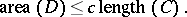This gives (further) geometric methods for studying hyperbolic groups.

References

[a1]	V.A. Ufnarovskii, "Combinatorial and asymptotic methods in algebra" A.I. Kostrikin (ed.) I.R. Shafarevich (ed.) , Algebra , VI , Springer (1995) (In Russian)
[a2]	R. Grigorchuk, T. Nagnibeda, "Operator growth functions of discrete groups" Invent. Math. (to appear)
[a3]	A.Yu. Ol'shanskii, "Geometry of defining relations in groups" , Kluwer Acad. Publ. (1991) (In Russian)
[a4]	M. Gromov, "Hyperboloic groups" , Essays in Group Theory , Springer (1987) pp. 75–263