Word metric
length metric
A metric on a finitely-generated group 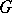 , defined as follows. Let
, defined as follows. Let 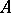 be a finite set of generators for
be a finite set of generators for 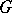 . Let
. Let 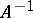 be the set of inverses of elements in
be the set of inverses of elements in 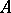 . If
. If 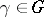 is not the identity element, then the length of
is not the identity element, then the length of 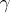 is defined as the minimal number of elements of
is defined as the minimal number of elements of 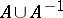 , counted with multiplicity, such that
, counted with multiplicity, such that 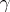 can be written as a product of these elements. The length of the identity element is defined to be zero. The word metric
can be written as a product of these elements. The length of the identity element is defined to be zero. The word metric 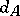 on
on 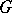 with respect to
with respect to 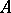 is then defined by the following formula: for all
is then defined by the following formula: for all 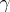 and
and 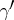 in
in 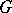 ,
, 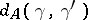 is equal to the length of the product
is equal to the length of the product 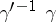 . The action of
. The action of 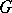 by left translations on the metric space
by left translations on the metric space 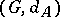 is an action by isometries. If
is an action by isometries. If 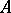 and
and 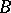 are two finite generating sets for
are two finite generating sets for 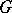 , then the identity mapping between the metric spaces
, then the identity mapping between the metric spaces 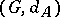 and
and 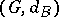 is a quasi-isometry.
is a quasi-isometry.
An equivalent definition is the following: 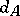 is the maximal metric on
is the maximal metric on 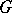 that is invariant by the left-action of
that is invariant by the left-action of 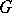 on itself, and such that the distance of any element of
on itself, and such that the distance of any element of 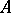 or
or 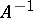 to the identity element of
to the identity element of 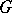 is equal to
is equal to 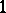 .
.
The notion of word metric lies at the foundation of geometric group theory. A group 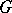 (equipped with a finite generating set
(equipped with a finite generating set 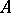 ) can be canonically imbedded, as the set of vertices, in the associated Cayley graph, which is a simplicial graph. This graph has a canonical metric, and the metric induced on the vertices is the word metric.
) can be canonically imbedded, as the set of vertices, in the associated Cayley graph, which is a simplicial graph. This graph has a canonical metric, and the metric induced on the vertices is the word metric.
The word metric on a group has much to do with the growth function of a finitely-generated group (cf. also Polynomial and exponential growth in groups and algebras; [a1], [a2]; see also [a3], especially Sect. 37, for other and related techniques in the study of groups).
Using the word metric (or the length of words), one defines
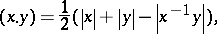 |
where 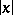 is the length of the element
is the length of the element 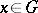 .
.
A group 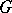 is hyperbolic (cf. also Hyperbolic group) if there is a constant
is hyperbolic (cf. also Hyperbolic group) if there is a constant 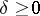 such that for all
such that for all 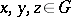 ,
,
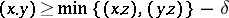 |
(cf. also [a1], [a4]). Hyperbolic groups are always finitely presented (cf. also Finitely-presented group), and as such realizable as the fundamental group of a smooth bounded region 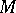 . Hyperbolicity is then equivalent to the purely geometric property that there is a constant
. Hyperbolicity is then equivalent to the purely geometric property that there is a constant  such that for every smooth closed curve
such that for every smooth closed curve 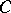 in
in 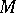 , contractible in
, contractible in 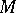 and bounding a disc
and bounding a disc 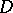 , one has
, one has
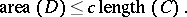 |
This gives (further) geometric methods for studying hyperbolic groups.
References
| [a1] | V.A. Ufnarovskii, "Combinatorial and asymptotic methods in algebra" A.I. Kostrikin (ed.) I.R. Shafarevich (ed.) , Algebra , VI , Springer (1995) (In Russian) |
| [a2] | R. Grigorchuk, T. Nagnibeda, "Operator growth functions of discrete groups" Invent. Math. (to appear) |
| [a3] | A.Yu. Ol'shanskii, "Geometry of defining relations in groups" , Kluwer Acad. Publ. (1991) (In Russian) |
| [a4] | M. Gromov, "Hyperboloic groups" , Essays in Group Theory , Springer (1987) pp. 75–263 |
Word metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Word_metric&oldid=18555