Skorokhod stochastic differential equation

An equation of the form

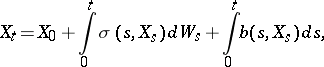(a1)

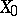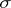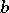where the initial condition and/or the coefficients and are random, the solution 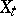is not adapted (cf. also Optional random process) to the Brownian motion 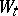, and the stochastic integral is interpreted in the sense of Skorokhod (see Skorokhod integral; Stochastic integral; [a5]). One cannot use a fixed-point argument to show the existence and uniqueness of the solution, as it is done for the adapted Itô stochastic equations, because the Skorokhod integral is not continuous in the 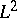-norm.

If 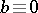, and 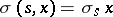, where 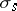is a deterministic function, (a1) has an explicit solution given by (see [a1])

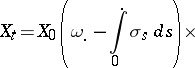(a2)

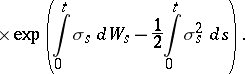When 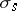is random, a similar formula holds but the martingale exponential should be replaced by the Girsanov density associated with the anticipating shift 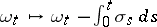(see [a3]).

Using the notion of Wick product, introduced in the context of quantum field theory, the process (a2) can be rewritten as

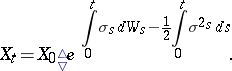(a3)

Formula (a3) can be used to solve linear multi-dimensional Skorokhod equations (see [a4]). One-dimensional non-linear Skorokhod stochastic differential equations are studied in [a2], and a local existence and uniqueness result is obtained by means of the pathwise representation of one-dimensional diffusions.

References

[a1]	R. Buckdahn, "Linear Skorohod stochastic differential equations" Probab. Th. Rel. Fields , 90 (1991) pp. 223–240
[a2]	R. Buckdahn, "Skorohod stochastic differential equations of diffusion type" Probab. Th. Rel. Fields , 92 (1993) pp. 297–324
[a3]	R. Buckdahn, "Anticipative Girsanov transformations and Skorohod stochastic differential equations" , Memoirs , 533 , Amer. Math. Soc. (1994)
[a4]	R. Buckdahn, D. Nualart, "Linear stochastic differential equations and Wick products" Probab. Th. Rel. Fields , 99 (1994) pp. 501–526
[a5]	A.V. Skorokhod, "On a generalization of a stochastic integral" Th. Probab. Appl. , 20 (1975) pp. 219–233