Saddle point in game theory

A point of a function defined on the Cartesian product of two sets and such that

(*)

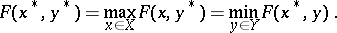For a function the presence of a saddle point is equivalent to the existence of optimal strategies (cf. Strategy (in game theory)) for the players in the two-person zero-sum game .

Comments

A point satisfying the condition (*) is called a saddle point of 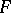in general. If is a differentiable function on 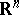and , , 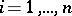while the Hessian matrix 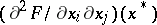is non-singular and neither positive definite nor negative definite, then locally near 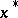, is a saddle point. The corresponding splitting of near is determined by the negative and positive eigenspaces of the Hessian at .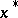

Indeed, by the Morse lemma there are coordinates near 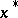such that 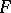has the form

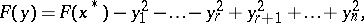where is the index of the quadratic form determined by the symmetric matrix 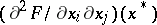. (The index of a quadratic form is the dimension of the largest subspace on which it is negative definite; this is also called the negative index of inertia (cf. also Quadratic form and Morse index).)

Let 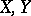be the spaces of strategies of two players in a zero-sum game and let 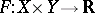be (the first component of) the pay-off function (cf. Games, theory of). Then a saddle point is also called an equilibrium point. This notion generalizes to -player non-cooperative games, cf. [a2], Chapt. 2; Games, theory of; Nash theorem (in game theory); Non-cooperative game.

References

[a1]	M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 6
[a2]	J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199