Blow-up algebra
Geometric description.
Associate to the punctured affine  -space
-space 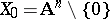 over
over 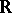 or
or 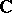 , the submanifold
, the submanifold 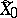 of
of 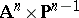 of points
of points 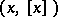 , where
, where  varies in
varies in 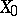 and
and 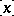 denotes the equivalence class of
denotes the equivalence class of  in the projective
in the projective 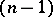 -dimensional space. The closure
-dimensional space. The closure 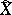 of
of 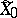 is smooth and is called the blow-up of
is smooth and is called the blow-up of 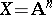 with centre the origin. In the real case and for
with centre the origin. In the real case and for 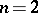 it is equal to the Möbius strip. The mapping
it is equal to the Möbius strip. The mapping 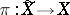 induced by the projection
induced by the projection 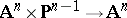 is an isomorphism over
is an isomorphism over 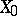 ; its fibre over
; its fibre over  is
is 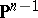 , the exceptional divisor of
, the exceptional divisor of 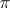 .
.
The strict transform 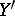 of a subvariety
of a subvariety 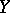 of
of 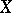 is the closure of the inverse image
is the closure of the inverse image 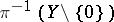 in
in 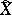 . For instance, if
. For instance, if 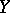 is the cuspidal curve
is the cuspidal curve 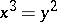 in
in 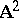 parametrized by
parametrized by 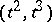 , then
, then 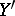 is given by
is given by 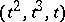 and hence is smooth. This forms the simplest example of resolution of singularities by a blow-up.
and hence is smooth. This forms the simplest example of resolution of singularities by a blow-up.
Higher-dimensional smooth centres 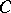 in
in 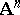 are blown up by decomposing
are blown up by decomposing 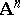 locally along
locally along 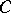 into a Cartesian product
into a Cartesian product 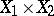 of submanifolds, where
of submanifolds, where 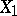 is transversal to
is transversal to 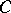 with
with 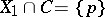 a point. Then
a point. Then 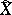 is given locally as
is given locally as 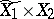 , where
, where 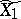 denotes the blow-up of
denotes the blow-up of 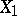 in
in 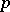 .
.
Algebraic description.
See also [a1]. Let 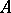 be a Noetherian ring and let
be a Noetherian ring and let 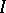 be an ideal of
be an ideal of 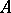 . Define the blow-up algebra (or Rees algebra) of
. Define the blow-up algebra (or Rees algebra) of 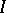 as the graded ring
as the graded ring 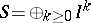 (where
(where 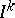 denotes the
denotes the 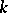 th power of
th power of 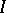 ,
, 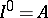 ). Then
). Then 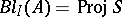 is the blow-up of
is the blow-up of 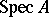 with centre
with centre 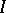 and coincides with the above construction when
and coincides with the above construction when 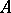 is the polynomial ring in
is the polynomial ring in  variables over
variables over 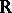 or
or 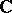 . Here,
. Here, 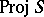 denotes the algebraic variety or scheme given by all homogeneous prime ideals of
denotes the algebraic variety or scheme given by all homogeneous prime ideals of 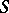 not containing the ideal
not containing the ideal 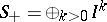 , and
, and 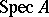 is the affine variety or scheme of all prime ideals of
is the affine variety or scheme of all prime ideals of 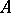 .
.
Local description.
Any generator system  of
of 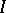 gives rise to a covering
gives rise to a covering
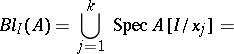 |
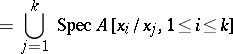 |
by 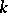 affine charts, the quotients
affine charts, the quotients 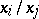 being considered as elements of the localization of
being considered as elements of the localization of 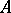 at
at 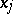 (cf. Localization in a commutative algebra). In the
(cf. Localization in a commutative algebra). In the 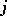 th chart
th chart 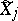 , the morphism
, the morphism 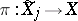 is induced by the inclusion
is induced by the inclusion 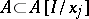 . For
. For 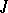 an ideal of
an ideal of 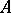 contained in
contained in 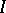 , the strict transform of
, the strict transform of 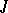 is
is 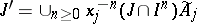 . The exceptional divisor has the equation
. The exceptional divisor has the equation 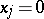 . If the centre
. If the centre 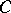 given by the ideal
given by the ideal 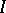 of
of 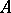 is smooth,
is smooth, 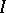 is generated by part of a regular parameter system of
is generated by part of a regular parameter system of 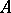 and
and 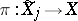 is given by
is given by 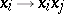 for
for 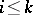 ,
, 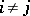 , and by
, and by 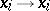 for
for 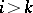 or
or  .
.
Properties.
Different centres may induce the same blow-up. A composite of blow-ups is again a blow-up. Blowing up commutes with base change; the strict transform of a variety equals its blow-up in the given centre. The morphism 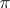 is birational, proper and surjective (cf. Birational morphism; Proper morphism; Surjection). Any birational projective morphism of quasi-projective varieties (cf. Quasi-projective scheme) is the blowing up of a suitable centre. The singularities of varieties over a field of characteristic
is birational, proper and surjective (cf. Birational morphism; Proper morphism; Surjection). Any birational projective morphism of quasi-projective varieties (cf. Quasi-projective scheme) is the blowing up of a suitable centre. The singularities of varieties over a field of characteristic  can be resolved by a finite sequence of blow-ups of smooth centres [a2]. In positive characteristic, this has only been proven for dimension
can be resolved by a finite sequence of blow-ups of smooth centres [a2]. In positive characteristic, this has only been proven for dimension 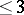 [a3]. See [a4] for a survey on resolution of singularities, and [a5] for an account on the role of blow-up algebras in commutative algebra.
[a3]. See [a4] for a survey on resolution of singularities, and [a5] for an account on the role of blow-up algebras in commutative algebra.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
| [a2] | H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero" Ann. of Math. , 79 (1964) pp. 109–326 MR0199184 Zbl 0122.38603 |
| [a3] | S. Abhyankar, "Resolution of singularities of embedded algebraic surfaces" , Acad. Press (1966) MR0217069 Zbl 0147.20504 |
| [a4] | J. Lipman, "Introduction to resolution of singularities" , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 187–230 MR0389901 Zbl 0306.14007 |
| [a5] | W. Vasconcelos, "Arithmetic of blowup algebras" , Lecture Notes Ser. , 195 , London Math. Soc. (1994) MR1275840 Zbl 0813.13008 |
Blow-up algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Blow-up_algebra&oldid=46087