Block
An ideal 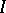 of a ring
of a ring 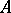 is said to be indecomposable if, for any ideals
is said to be indecomposable if, for any ideals 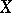 and
and 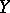 of
of 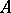 ,
, 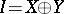 implies
implies 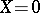 or
or 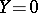 . The ideal
. The ideal 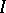 is called a direct summand of
is called a direct summand of 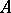 if
if 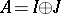 for some ideal
for some ideal 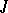 of
of 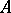 . A block of
. A block of 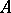 is defined to be any ideal of
is defined to be any ideal of 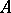 which is an indecomposable direct summand of
which is an indecomposable direct summand of 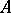 . By a block idempotent of
. By a block idempotent of 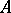 one understands any primitive idempotent of the centre of
one understands any primitive idempotent of the centre of 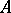 (cf. also Centre of a ring). An ideal
(cf. also Centre of a ring). An ideal 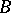 of
of 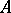 is a block of
is a block of 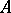 if and only if
if and only if 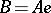 for some (necessarily unique) block idempotent
for some (necessarily unique) block idempotent  of
of 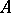 . Thus blocks and block idempotents determine each other.
. Thus blocks and block idempotents determine each other.
Any decomposition of 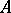 of the form
of the form 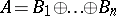 , where each
, where each 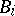 is a block of
is a block of 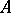 , is called a block decomposition of
, is called a block decomposition of 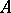 . In general, such a decomposition need not exist, but it does exist if
. In general, such a decomposition need not exist, but it does exist if 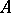 is semi-perfect (cf. Perfect ring). In the classical case where
is semi-perfect (cf. Perfect ring). In the classical case where 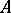 is semi-primitive Artinian (cf. Primitive ring; Artinian ring), each block of
is semi-primitive Artinian (cf. Primitive ring; Artinian ring), each block of 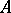 is a complete matrix ring over a suitable division ring, and the number of blocks of
is a complete matrix ring over a suitable division ring, and the number of blocks of 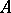 is equal to the number of non-isomorphic simple
is equal to the number of non-isomorphic simple 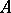 -modules.
-modules.
The study of blocks is especially important in the context of group representation theory (see Representation of a group; [a1], [a2], [a3], [a4], [a5]). Here, the role of 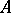 is played by the group algebra
is played by the group algebra 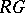 , where
, where 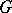 is a finite group and the commutative ring
is a finite group and the commutative ring 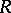 is assumed to be a complete Noetherian semi-local ring (cf. also Commutative ring; Noetherian ring; Local ring) such that
is assumed to be a complete Noetherian semi-local ring (cf. also Commutative ring; Noetherian ring; Local ring) such that 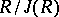 has prime characteristic
has prime characteristic 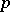 . The most important special cases are:
. The most important special cases are:
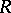 is a complete discrete valuation ring of characteristic
is a complete discrete valuation ring of characteristic  with
with 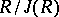 of prime characteristic
of prime characteristic 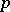 ;
;
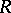 is a field of prime characteristic
is a field of prime characteristic 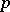 .
.
One of the most useful aspects of modular representation theory is the study of the distribution of the irreducible ordinary characters of 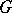 into blocks. The main idea is due to R. Brauer and can be described as follows. Let
into blocks. The main idea is due to R. Brauer and can be described as follows. Let 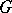 be a finite group and let
be a finite group and let 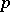 be a prime number. Assume that
be a prime number. Assume that 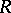 is a complete discrete valuation ring of characteristic
is a complete discrete valuation ring of characteristic  ,
, 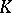 is the quotient field of
is the quotient field of 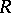 and
and 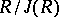 is of characteristic
is of characteristic 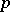 . Let
. Let 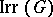 be the set of all irreducible
be the set of all irreducible 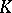 -characters of
-characters of 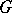 (cf. Character of a group) and write
(cf. Character of a group) and write 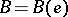 to indicate that
to indicate that 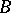 is a block of
is a block of 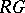 whose corresponding block idempotent is
whose corresponding block idempotent is  , i.e.,
, i.e., 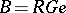 . The character
. The character 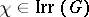 is said to belong to the block
is said to belong to the block 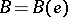 of
of 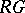 if
if 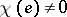 (here
(here 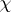 is extended by
is extended by 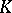 -linearity to the mapping
-linearity to the mapping 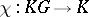 ). It turns out that if
). It turns out that if 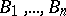 are all distinct blocks of
are all distinct blocks of 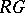 , then
, then 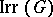 is a disjoint union of the
is a disjoint union of the 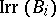 ,
, 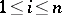 , where
, where 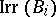 denotes the set of irreducible
denotes the set of irreducible 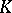 -characters of
-characters of 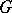 belonging to
belonging to 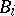 . In the classical case studied by Brauer, namely when
. In the classical case studied by Brauer, namely when 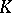 is a splitting field for
is a splitting field for 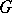 , the irreducible
, the irreducible 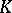 -characters of
-characters of 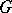 are identifiable with the irreducible
are identifiable with the irreducible 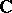 -characters of
-characters of 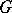 .
.
Assume that, in the context of the previous paragraph, 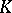 is a splitting field for
is a splitting field for 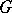 . Let
. Let  be a block of
be a block of 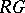 and let
and let 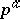 be the order of Sylow
be the order of Sylow 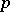 -subgroups of
-subgroups of 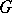 (cf. Sylow subgroup). It turns out that there exists an integer
(cf. Sylow subgroup). It turns out that there exists an integer 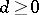 , called the defect of
, called the defect of 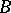 , such that
, such that 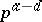 is the largest power of
is the largest power of 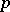 which divides
which divides 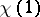 for all
for all 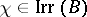 . The notion of the defect of
. The notion of the defect of 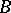 can be defined by purely ring-theoretic properties under much more general circumstances. Namely, it suffices to assume that
can be defined by purely ring-theoretic properties under much more general circumstances. Namely, it suffices to assume that 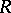 is a complete Noetherian semi-local ring such that
is a complete Noetherian semi-local ring such that 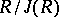 has prime characteristic
has prime characteristic 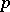 (see [a5]; Noetherian ring).
(see [a5]; Noetherian ring).
For the classical case where 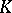 is a splitting field for
is a splitting field for 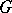 , one has the following famous problem, frequently called the Brauer
, one has the following famous problem, frequently called the Brauer 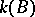 -conjecture. Let
-conjecture. Let 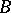 be a block of
be a block of 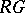 and let
and let 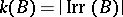 . Is it true that
. Is it true that 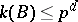 , where
, where 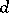 is the defect of
is the defect of 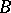 ? Although many special cases have been attacked successfully, the general case is still far from being solved. So far (1996), Brauer's
? Although many special cases have been attacked successfully, the general case is still far from being solved. So far (1996), Brauer's 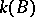 -conjecture has not been verified for all finite simple groups. Moreover, it is not known whether Brauer's
-conjecture has not been verified for all finite simple groups. Moreover, it is not known whether Brauer's 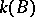 -conjecture can be reduced to the case of simple (or at least quasi-simple) groups (see [a5]).
-conjecture can be reduced to the case of simple (or at least quasi-simple) groups (see [a5]).
References
| [a1] | G. Karpilovsky, "Group representations" , 1 , North-Holland (1992) |
| [a2] | G. Karpilovsky, "Group representations" , 2 , North-Holland (1993) |
| [a3] | G. Karpilovsky, "Group representations" , 3 , North-Holland (1994) |
| [a4] | G. Karpilovsky, "Group representations" , 4 , North-Holland (1995) |
| [a5] | G. Karpilovsky, "Group representations" , 5 , North-Holland (1996) |
Block. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Block&oldid=46085