Kirillov conjecture
From Encyclopedia of Mathematics
Let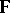 
be a local field and 
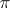an irreducible unitary representation of 
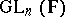. Let
 |
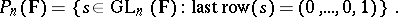Then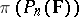 
is irreducible (cf. also Irreducible representation).
A related conjecture is that for two irreducible representations 
and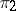 
of, respectively, 
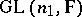and 
, the product
 |
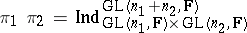is irreducible.
For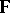 
non-Archimedean (cf. also Archimedean axiom), both conjectures are true (Bernstein's theorems).
For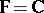 
, these conjectures have been proved by S. Sahi [a1].
References
| [a1] | S. Sahi, "On Kirillov's conjecture for Archimedean fields" Compositio Math. , 72 : 1 (1989) pp. 67–86 |
How to Cite This Entry:
Kirillov conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kirillov_conjecture&oldid=42875
Kirillov conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kirillov_conjecture&oldid=42875
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article