Bernoulli excursion
Consider a set of sequences each consisting of 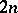 elements such that
elements such that  elements are equal to
elements are equal to 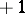 ,
,  elements are equal to
elements are equal to 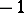 , and the sum of the first
, and the sum of the first 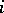 elements is greater than or equal to zero for every
elements is greater than or equal to zero for every 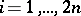 . The number of such sequences is given by the
. The number of such sequences is given by the  th Catalan number{}
th Catalan number{}
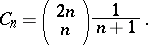 |
The first few Catalan numbers are: 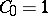 ,
, 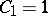 ,
, 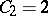 ,
, 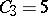 ,
, 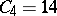 ,
, 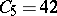 . A sequence is randomly chosen from the
. A sequence is randomly chosen from the 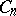 sequences, assuming that all possible sequences are equally probable. Denote by
sequences, assuming that all possible sequences are equally probable. Denote by 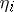 (
( ) the sum of the first
) the sum of the first 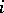 elements in this chosen sequence and set
elements in this chosen sequence and set 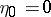 . Then
. Then 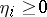 for
for 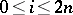 and
and 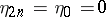 . The sequence
. The sequence 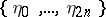 describes a random walk, which is usually called a Bernoulli excursion (cf. also Bernoulli random walk). One can imagine that a particle performs a random walk on the
describes a random walk, which is usually called a Bernoulli excursion (cf. also Bernoulli random walk). One can imagine that a particle performs a random walk on the  -axis. It starts at
-axis. It starts at 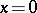 and takes
and takes 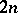 steps. At the
steps. At the 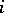 th step the particle moves either a unit distance to the right or a unit distance to the left according to whether the
th step the particle moves either a unit distance to the right or a unit distance to the left according to whether the 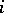 th element in the random sequence is
th element in the random sequence is 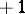 or
or 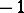 . At the end of the
. At the end of the 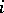 th step the position of the particle is
th step the position of the particle is 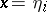 for
for 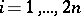 .
.
In probability theory, many problems require the determination of the distributions of various functionals of the Bernoulli excursion. For example, for a single-server queue 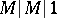 the distribution of the maximal queue size during a busy period requires the determination of the distribution of the random variable
the distribution of the maximal queue size during a busy period requires the determination of the distribution of the random variable 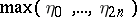 . Another example is concerned with random trees. There are
. Another example is concerned with random trees. There are 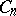 complete binary rooted plane trees with
complete binary rooted plane trees with 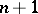 unlabelled vertices. Choose a tree at random, assuming that all the
unlabelled vertices. Choose a tree at random, assuming that all the 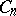 possible trees are equally probable. Then the height of the random tree has the same distribution as
possible trees are equally probable. Then the height of the random tree has the same distribution as  in the Bernoulli excursion. Explicitly:
in the Bernoulli excursion. Explicitly:
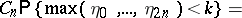 |
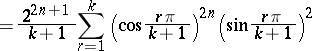 |
for 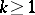 and
and 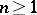 . For other examples see [a1], [a2].
. For other examples see [a1], [a2].
References
| [a1] | L. Takács, "A Bernoulli excursion and its various applications" Adv. in Probability , 23 (1991) pp. 557–585 |
| [a2] | L. Takács, "Queueing methods in the theory of random graphs" J.H. Dshalalow (ed.) , Advances in Queueing Theory, Methods, and Open Problems , CRC (1995) pp. 45–78 |
Bernoulli excursion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_excursion&oldid=42607