Gamma-invariant in the theory of Abelian groups
 -invariant
-invariant
An invariant associated to an uncountable Abelian group and taking values in a Boolean algebra. Two groups with different invariants are non-isomorphic, but the converse fails in general: groups with the same invariant need not be isomorphic. The invariant is most commonly defined for almost-free groups (groups such that every subgroup of strictly smaller cardinality is a free Abelian group). By a theorem of S. Shelah (see [a7]), such a group is free if it is of singular cardinality, so the invariant is defined for groups of regular cardinality (see Cardinal number). If  is an Abelian group of regular uncountable cardinality
is an Abelian group of regular uncountable cardinality  ,
,  is said to be
is said to be  -free if and only if every subgroup of
-free if and only if every subgroup of  of cardinality
of cardinality  is free. In that case
is free. In that case  can be written as the union of a continuous chain (called a
can be written as the union of a continuous chain (called a 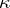 -filtration) of free subgroups of cardinality
-filtration) of free subgroups of cardinality  :
: 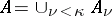 , where the continuity condition means that for every limit ordinal
, where the continuity condition means that for every limit ordinal  ,
,  . The
. The  -invariant of
-invariant of  , denoted by
, denoted by  or just
or just  , is defined to be the equivalence class,
, is defined to be the equivalence class,  , of
, of
 |
 is defined to be the set of all subsets
is defined to be the set of all subsets  of
of  for which
for which  for some closed unbounded subset
for some closed unbounded subset 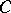 of
of  . (See Suslin hypothesis for the definitions of closed unbounded and stationary.) The equivalence class depends only on the isomorphism type of
. (See Suslin hypothesis for the definitions of closed unbounded and stationary.) The equivalence class depends only on the isomorphism type of 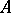 and not on the choice of
and not on the choice of  -filtration, because any two
-filtration, because any two  -filtrations agree on a closed unbounded subset of
-filtrations agree on a closed unbounded subset of  ; the equivalence classes of subsets of
; the equivalence classes of subsets of 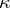 form a Boolean algebra,
form a Boolean algebra, 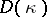 , under the partial order induced by inclusion. The least element of this Boolean algebra,
, under the partial order induced by inclusion. The least element of this Boolean algebra,  , is the class of all non-stationary subsets of
, is the class of all non-stationary subsets of  . It can be proved that
. It can be proved that  if and only if
if and only if  is free (see [a1]). For
is free (see [a1]). For  (
(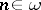 ), every one of the
), every one of the 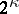 members of the Boolean algebra
members of the Boolean algebra  is the
is the 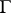 -invariant of some
-invariant of some  -free group of cardinality
-free group of cardinality  (see [a6]). Assuming Gödel's axiom of constructibility,
(see [a6]). Assuming Gödel's axiom of constructibility,  (see Gödel constructive set), the same holds for all regular
(see Gödel constructive set), the same holds for all regular 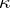 which are not too large (e.g., less than the first inaccessible cardinal, or even the first Mahlo cardinal); in fact, a complete characterization, for any regular
which are not too large (e.g., less than the first inaccessible cardinal, or even the first Mahlo cardinal); in fact, a complete characterization, for any regular  , of the range of
, of the range of 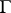 can be given, assuming
can be given, assuming  (see [a6] and [a5]).
(see [a6] and [a5]).
Another 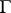 -invariant can be defined for use in connection with the Whitehead problem in Abelian group theory, and its generalizations. In this case, for any Abelian groups
-invariant can be defined for use in connection with the Whitehead problem in Abelian group theory, and its generalizations. In this case, for any Abelian groups  and
and  ,
,  is defined to be the equivalence class of
is defined to be the equivalence class of
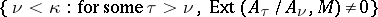 |
when 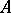 is
is  -free of cardinality
-free of cardinality 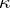 and
and  is written as the union,
is written as the union,  , of a
, of a  -filtration. Then
-filtration. Then  implies
implies  ; the converse holds for
; the converse holds for 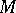 of cardinality at most
of cardinality at most  , assuming
, assuming  (see [a2]).
(see [a2]).
Useful references for additional information are [a3] and [a4].
References
| [a1] | P.C. Eklof, "Methods of logic in abelian group theory" , Abelian Group Theory , Lecture Notes in Mathematics , 616 , Springer (1977) pp. 251–269 |
| [a2] | P.C. Eklof, "Homological algebra and set theory" Trans. Amer. Math. Soc. , 227 (1977) pp. 207–225 |
| [a3] | P.C. Eklof, "Set-theoretic methods: the uses of gamma invariants" , Abelian Groups , Lecture Notes in Pure and Appl. Math. , 146 , M. Dekker (1993) pp. 143–153 |
| [a4] | P.C. Eklof, A.H. Mekler, "Almost free modules" , North-Holland (1990) |
| [a5] | P.C. Eklof, A.H. Mekler, S. Shelah, "Almost disjoint abelian groups" Israel J. Math. , 49 (1984) pp. 34–54 |
| [a6] | A.H. Mekler, "How to construct almost free groups" Canad. J. Math. , 32 (1980) pp. 1206–1228 |
| [a7] | S. Shelah, "A compactness theorem for singular cardinals, free algebras, Whitehead problem and transversals" Israel J. Math. , 21 (1975) pp. 319–349 |
Gamma-invariant in the theory of Abelian groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gamma-invariant_in_the_theory_of_Abelian_groups&oldid=42426