Ricci tensor
From Encyclopedia of Mathematics
A twice-covariant tensor obtained from the Riemann tensor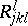 
by contracting the upper index with the first lower one:
 |
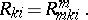In a Riemannian space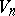 
the Ricci tensor is symmetric: 
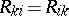. The trace of the Ricci tensor with respect to the contravariant metric tensor 
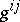of the space 
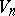leads to a scalar, 
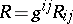, called the curvature invariant or the scalar curvature of 
. The components of the Ricci tensor can be expressed in terms of the metric tensor 
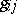of the space 
:
 |
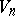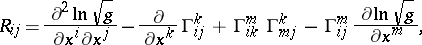where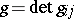 
and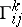 
are the Christoffel symbols of the second kind (cf. Christoffel symbol) calculated with respect to the tensor 
.
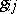The tensor was introduced by G. Ricci [1].
References
| [1] | G. Ricci, Atti R. Inst. Venelo , 53 : 2 (1903–1904) pp. 1233–1239 |
| [2] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) |
Comments
References
| [a1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) |
How to Cite This Entry:
Ricci tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ricci_tensor&oldid=38665
Ricci tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ricci_tensor&oldid=38665
This article was adapted from an original article by L.A. Sidorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article