Green space

A topological space on which harmonic and superharmonic functions (cf. Harmonic function; Subharmonic function) are defined and for which a Green function exists (for the Dirichlet problem in the class of harmonic functions) or, which amounts to the same thing, for which there exists a non-constant superharmonic function. More exactly, let be an -space, i.e. a connected separable topological space in which: 1) each point has an open neighbourhood homeomorphic to some open set of a Euclidean space (or of its Aleksandrov compactification ); and 2) the images of any non-empty intersection (under the two homeomorphisms to 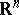or 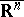) of two neighbourhoods in and 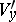are isometric, and are conformally equivalent if . Harmonic and superharmonic functions on an 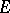-space are locally defined by passing to the images . If, in addition, there exists a non-constant positive superharmonic function on or, which amounts to the same thing, a positive potential, is known as a Green space. Thus, the Euclidean space , its compactification (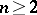) and Riemann surfaces are all -spaces. Here, and Riemann surfaces of hyperbolic type (cf. Riemann surfaces, classification of) are Green spaces, while and Riemann surfaces of parabolic type are not. Any domain in a Green space is again a Green space.

A harmonic space 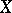with a positive potential on it can also be regarded as a generalization of a Green space in the framework of axiomatic potential theory (cf. Potential theory, abstract).

References

[1]	M. Brelot, "On topologies and boundaries in potential theory" , Springer (1971)
[2]	M. Brélot, G. Choquet, "Espaces et lignes de Green" Ann. Inst. Fourier , 3 (1952) pp. 199–263