Completion, MacNeille (of a partially ordered set)

completion by sections

The complete lattice 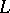obtained from a partially ordered set 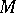in the following way. Let 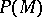be the set of all subsets of 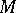, ordered by inclusion. For any 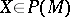assume that

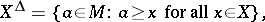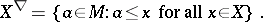The condition 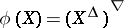defines a closure operation (cf. Closure relation) 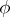on . The lattice 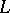of all 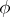-closed subsets of 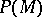is complete. For any 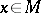the set 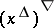is the principal ideal generated by . Put 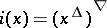for all 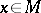. Then 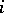is an isomorphic imbedding of 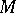into the complete lattice 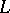that preserves all least upper bounds and greatest lower bounds existing in 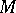. When applied to the ordered set of rational numbers, the construction described above gives the completion of the set of rational numbers by Dedekind sections.

References

[1]	H.M. MacNeille, "Partially ordered sets" Trans. Amer. Math. Soc. , 42 (1937) pp. 416–460

Comments

The MacNeille completion of a Boolean algebra is a (complete) Boolean algebra, but the MacNeille completion of a distributive lattice need not be distributive (see [a1]). When restricted to Boolean algebras the MacNeille completion corresponds by Stone duality (cf. Stone space) to the construction of the absolute (or the Gleason cover construction) for compact zero-dimensional spaces (cf. Zero-dimensional space; [a2], p. 109).

References

[a1]	S.P. Crawley, "Regular embeddings which preserve lattice structure" Proc. Amer. Math. Soc. , 13 (1962) pp. 748–752
[a2]	P.T. Johnstone, "Stone spaces" , Cambridge Univ. Press (1982)