Floquet exponents

Exponents arising in the study of solutions of a linear ordinary differential equation invariant with respect to a discrete Abelian group (cf. also Floquet theory). The simplest example is a periodic ordinary differential equation

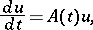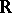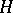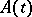where is a vector function on with values in a finite-dimensional complex vector space and is an 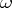-periodic function with values in the space of linear operators in 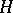. The space of solutions of this equation is finite-dimensional and invariant with respect to the action 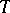of the integer group 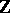by shifts

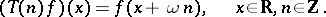Here, is the monodromy operator. One can expand any solution into eigenvectors and generalized eigenvectors of (cf. also Eigen vector). This amounts to expanding the action of 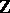on the solution space into irreducible and primary representations (cf. also Representation of a group). If 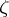is an eigen value of 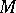and 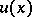is the corresponding eigenvector, then

The number 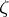is the Floquet multiplier of . Since , , 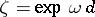where is the Floquet exponent. The solution (called the Floquet solution, or the Bloch solution in physics) can be represented as

with an 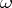-periodic function 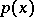. The generalized eigenvectors can be written as

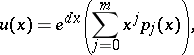with an 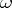-periodic . Floquet solutions play a major role in any considerations involving periodic ordinary differential equations, similar to exponential-polynomial solutions in the constant-coefficient case. This approach to periodic ordinary differential equations was developed by G. Floquet [a4]. One can find detailed description and applications of this theory in many places, for instance in [a3] and [a7].

The Floquet theory can, to some extent, be carried over to the case of evolution equations in infinite-dimensional spaces with bounded or unbounded operator coefficient 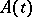(for instance, for the time-periodic heat equation; cf. also Heat equation). One can find discussion of this matter in [a5] and [a2].

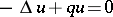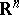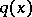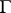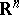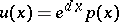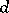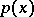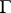Consider now the case of a partial differential equation periodic with respect to several variables. Among the most important examples arising in applications is the Schrödinger equation in with a potential that is periodic with respect to a lattice in [a1]. A Floquet solution has the form , where the Floquet exponent is a vector and the function is -periodic. One should note that in physics the vector 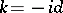is called the quasi-momentum [a1]. Transfer of Floquet theory to the case of spatially periodic partial differential equations is possible, but non-trivial. For instance, one cannot use the monodromy operator (see [a3] and [a6] for the Schrödinger case and [a5] for more general considerations).

In some cases an equation can be periodic with respect to an Abelian group whose action is not just translation. Consider the magnetic Schrödinger operator

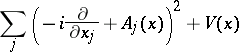and define the differential form 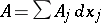. Assume that the electric potential and the magnetic field 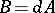are periodic with respect to a lattice 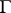. This does not guarantee periodicity of the equation itself. However, if one combines shifts by elements of 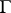with appropriate phase shifts, one gets a discrete group (cf. also Discrete subgroup) with respect to which the equation is invariant. This group is non-commutative in general [a8], so the standard Floquet theory does not apply. However, under a rationality condition, the group is commutative and a version of magnetic Floquet theory is applicable [a8].

References

[a1]	N.W. Ashcroft, N.D. Mermin, "Solid State Physics" , Holt, Rinehart&Winston (1976)
[a2]	Ju.L. Daleckii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Transl. Math. Monogr. , 43 , Amer. Math. Soc. (1974)
[a3]	M.S.P. Eastham, "The spectral theory of periodic differential equations" , Scottish Acad. Press (1973)
[a4]	G. Floquet, "Sur les equations differentielles lineaires a coefficients periodique" Ann. Ecole Norm. Ser. 2 , 12 (1883) pp. 47–89
[a5]	P. Kuchment, "Floquet theory for partial differential equations" , Birkhäuser (1993)
[a6]	M. Reed, B. Simon, "Methods of modern mathematical physics: Analysis of operators" , IV , Acad. Press (1978)
[a7]	V.A. Yakubovich, V.M. Starzhinskii, "Linear differential equations with periodic coefficients" , 1, 2 , Halsted Press&Wiley (1975)
[a8]	J. Zak, "Magnetic translation group" Phys. Rev. , 134 (1964) pp. A1602–A1611