Imbedding of rings

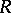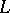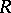A monomorphism of a ring into another ring; a ring is imbeddable in a ring if is isomorphic to a subring of 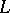. The conditions for imbedding of an associative ring in an (associative) skew-field and of an arbitrary ring into a division ring have been studied in great detail. These studies were initiated by A.I. Mal'tsev [1], who constructed an example of an associative ring without zero divisors and not imbeddable in a skew-field. The following Mal'tsev problem remained an open question for a long time: Is any associative ring without zero divisors and for which the semi-group of non-zero elements is imbeddable in a group, imbeddable in a skew-field? This problem was negatively answered in 1966 (cf. [2]). A square matrix 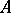of order 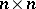over an associative ring 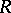is said to be non-full if it can be represented in the form 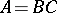where 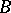, 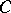are matrices of orders 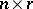and 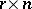, respectively, and 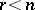. Let

be square matrices of ord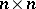er over 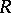in which all columns (except, possibly, the first column) are identical. Then the matrix

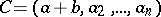is said to be the determinant sum of 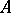and 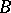with respect to the first column. The determinant sum of square matrices of the same order with respect to an arbitrary column (row) is defined in a similar manner. An associative ring 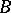with a unit element is imbeddable in a skew-field if and only if it has no zero divisors and if no scalar matrix 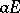with a non-zero element along the diagonal can be represented as the determinant sum of a finite number of non-full matrices [2]. The class of associative rings imbeddable in skew-fields is not finitely axiomatized (i.e. cannot be defined by a finite number of axioms) [3]. A number of sufficient conditions for imbedding of an associative ring in a skew-field are known; the following are the most important. Let 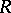be an associative ring without zero divisors and for which the semi-group of non-zero elements satisfies Ore's condition (cf. Imbedding of semi-groups). Then 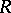is imbeddable in a skew-field [4]. The group algebra of an ordered group is imbeddable in a skew-field (the Mal'tsev–Neumann theorem, cf. [4]). An arbitrary domain of free right (left) ideals (cf. Associative rings and algebras) is imbeddable in a skew-field [2].

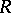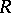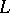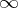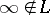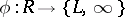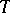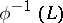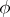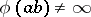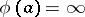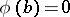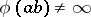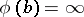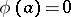A ring is imbeddable in a division ring if and only if it has no zero divisors. Let , be rings, let be a symbol, . A mapping is said to be a -homomorphism if: 1) the set is a ring and the mapping on this set is a ring homomorphism; 2) it follows from , that ; and 3) it follows from , that . A 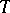-homomorphism of a field is nothing but a specialization (of a point) of the field (cf. Specialization of a point). A division ring 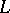is a free 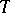-extension of a ring 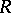if 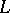includes 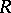and is generated (as a division ring) by the ring 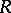, while any 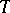-homomorphism of the ring 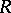into some division ring 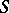may be extended to a 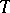-homomorphism of 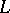into 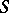. Every ring without zero divisors has a free 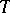-extension [4].

References

[1]	A.I. [A.I. Mal'tsev] Malcev, "On the immersion of an algebraic ring into a field" Math. Ann. , 113 (1937) pp. 686–691
[2]	P.M. Cohn, "Free rings and their relations" , Acad. Press (1971)
[3]	P.M. Cohn, "The class of rings embeddable in skew fields" Bull. London Math. Soc. , 6 (1974) pp. 147–148
[4]	P.M. Cohn, "Universal algebra" , Reidel (1981)
[5]	L.A. Bokut', "Embedding of rings" Russian Math. Surveys , 42 : 4 (1987) pp. 105–138 Uspekhi Mat. Nauk , 42 (1987) pp. 87–111

Comments

A 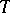-homomorphism is also called a localization (cf. also Localization in a commutative algebra).

Another classical problem is imbedding of a ring 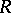in a finite matrix ring over a commutative ring. A necessary condition is that it satisfies all universal polynomial identities 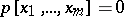of the 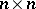matrix ring over the integers. The condition is sufficient if is prime or semi-prime, but fails in other cases (cf. [a1]).

References

[a1]	L.H. Rowen, "Polynomial identities in ring theory" , Acad. Press (1980) pp. Chapt. 7