Locally compact space
A topological space at every point of which there is a neighbourhood with compact closure. A locally compact Hausdorff space  is a completely-regular space. The partially ordered set of all its Hausdorff compactifications (cf. Compactification) is a complete lattice. Its minimal element is the Aleksandrov compactification
is a completely-regular space. The partially ordered set of all its Hausdorff compactifications (cf. Compactification) is a complete lattice. Its minimal element is the Aleksandrov compactification  . The class of locally compact Hausdorff spaces coincides with the class of open subsets of Hausdorff compacta. For a locally compact Hausdorff space
. The class of locally compact Hausdorff spaces coincides with the class of open subsets of Hausdorff compacta. For a locally compact Hausdorff space 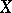 its remainder
its remainder  in any Hausdorff compactification
in any Hausdorff compactification  is a Hausdorff compactum. Every connected paracompact locally compact space is the sum of countably many compact subsets.
is a Hausdorff compactum. Every connected paracompact locally compact space is the sum of countably many compact subsets.
The most important example of a locally compact space is  -dimensional Euclidean space. A topological Hausdorff vector space
-dimensional Euclidean space. A topological Hausdorff vector space  (not reducing to the zero element) over a complete non-discretely normed division ring
(not reducing to the zero element) over a complete non-discretely normed division ring  is locally compact if and only if
is locally compact if and only if  is locally compact and
is locally compact and  is finite-dimensional over
is finite-dimensional over  .
.
Comments
A product  of topological spaces is locally compact if and only if each separate coordinate space
of topological spaces is locally compact if and only if each separate coordinate space  is locally compact and all but finitely many are compact.
is locally compact and all but finitely many are compact.
References
| [a1] | J.L. Kelley, "General topology" , v. Nostrand (1955) pp. 146–147 |
Locally compact space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_compact_space&oldid=32382