Tetrahedral coordinates
From Encyclopedia of Mathematics
of a point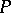 
in three-dimensional space
Numbers 
which are proportional (with given coefficient of proportionality) to the distances from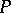 
to the faces of a fixed tetrahedron, not necessarily regular. Analogously, one may introduce general normal coordinates for any dimension. The two-dimensional analogues of tetrahedral coordinates are called trilinear coordinates. See also Barycentric coordinates.
Comments
References
| [a1] | H.S.M. Coxeter, "Regular polytopes" , Dover, reprint (1973) pp. 183 |
How to Cite This Entry:
Tetrahedral coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tetrahedral_coordinates&oldid=31739
Tetrahedral coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tetrahedral_coordinates&oldid=31739
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article