Histogram
A method for representing experimental data. A histogram is constructed as follows. The entire range of the observed values 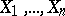 of some random variable
of some random variable 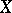 is subdivided into
is subdivided into 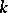 grouping intervals (which are usually all of equal length) by points
grouping intervals (which are usually all of equal length) by points 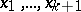 ; the number of observations
; the number of observations 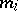 per interval
per interval 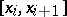 and the frequency
and the frequency 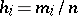 are computed. The points
are computed. The points  are marked on the abscissa, and the segments
are marked on the abscissa, and the segments 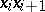 (
( ) are taken as the bases of rectangles with heights
) are taken as the bases of rectangles with heights 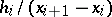 . If the intervals
. If the intervals 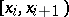 have equal lengths, the altitudes of the rectangles are taken as
have equal lengths, the altitudes of the rectangles are taken as 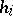 or as
or as 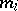 . Thus, let the measurements of trunks of 1000 firs give the following results:'
. Thus, let the measurements of trunks of 1000 firs give the following results:'
<tbody> </tbody>
|
The histogram for this example is shown in the figure. diameter in cm. number of trunks
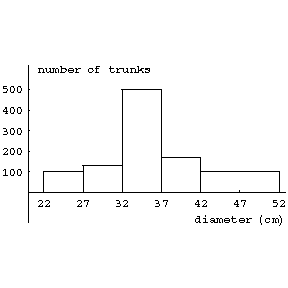
Figure: h047450a
Comments
The histogram can be considered as a technique of density estimation (cf. also Density of a probability distribution), and there is much literature on its properties as a statistical estimator of an unknown probability density as  and the grouping intervals are made smaller (grouping intervals of lengths
and the grouping intervals are made smaller (grouping intervals of lengths 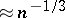 seem optimal).
seem optimal).
References
| [a1] | D. Freedman, P. Diaconis, "On the histogram as a density estimator:  theory" Z. Wahrsch. Verw. Geb. , 57 (1981) pp. 453–476 theory" Z. Wahrsch. Verw. Geb. , 57 (1981) pp. 453–476 |
Histogram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Histogram&oldid=29843