Nash theorems (in differential geometry)

Two groups of theorems on isometrically imbedded and immersed Riemannian manifolds in a Euclidean space (see also Immersion of a manifold; Isometric immersion). The original versions are due to J. Nash [1].

1) Nash' theorem on 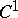-imbeddings and 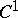-immersions. An immersion (imbedding) 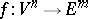of class 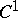of an -dimensional Riemannian space 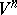with metric 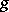of class 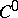into an 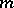-dimensional Euclidean space 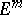is called short if the metric 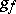induced by it on 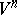is such that the quadratic form 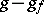is positive definite. If 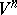has a short immersion (imbedding) in 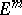, , 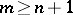then 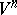also has an isometric immersion (imbedding) of class 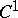in 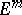. Under the restriction 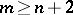this theorem was proved in [1], and in the form stated above in [2]. This theorem implies, in particular, that if a compact Riemannian manifold 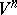has a 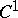-imbedding (immersion) in 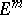, , 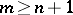then 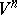also has an isometric 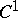-imbedding (immersion) in 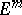. Another consequence of Nash' theorem is that every point of 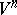has a sufficiently small neighbourhood that admits an isometric imbedding of class 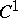in .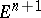

2) Nash' theorem on regular imbeddings. Every compact Riemannian manifold 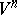of class 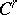, , 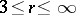has an isometric 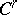-imbedding in 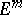, where 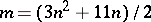. If 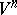is not compact, then it has an isometric 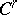-imbedding in 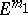, where .

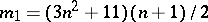Nash' theorem on regular imbeddings results from an application of Nash' implicit-function theorem on the inversion of a broad class of differential operators. The meaning of this theorem is that when a certain linear algebraic system of equations connected naturally with a differential operator 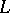is solvable and when a reasonable topology is introduced in the image and inverse image, then the operator in question is an open mapping, that is, 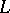is locally invertible near any point of its range. For the equations of an imbedding of a Riemannian manifold in a Euclidean space this reduces to the fact that the first and second derivatives of the mapping 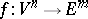with respect to the intrinsic coordinates of 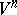must be linearly independent. Such imbeddings were first considered in [4]; they are called free. Nash' implicit-function theorem implies that a compact Riemannian manifold 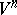sufficiently close to another one 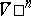having a free imbedding in 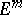also has a free imbedding in 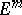. This fact and the original method of extension with respect to a parameter lead to Nash' theorem on regular imbeddings (see [3]). By extending Nash' method to non-compact manifolds and analytic imbeddings, and also by a principal refinement of the process of extension with respect to a parameter, it has been proved that every infinitely-differentiable (analytic) Riemannian manifold 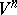has an isometric differentiable (analytic) imbedding in 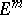, where 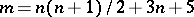(see [5]–[7]).

References

[1]	J. Nash, "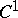-isometric imbeddings" Ann. of Math. , 60 (1954) pp. 383–396
[2]	N. Kuiper, "On 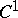-isometric imbeddings" Proc. K. Ned. Akad. Wetensch. , A58 : 4 (1955) pp. 545–556
[3]	J. Nash, "The imbedding problem for Riemannian manifolds" Ann. of Math. , 63 (1956) pp. 20–63
[4]	C. Burstin, "Ein Beitrag zum Problem der Einbettung der Riemannschen Räume in euklidischen Räumen" Mat. Sb. , 38 : 3–4 (1931) pp. 74–85
[5]	J. Nash, "Analyticity of the solutions of implicit function problems with analytic data" Ann. of Math. , 84 (1966) pp. 345–355
[6]	M.L. Gromov, V.A. Rokhlin, "Embeddings and immersions in Riemannian geometry" Russian Math. Surveys , 25 : 5 (1970) pp. 1–57 Uspekhi Mat. Nauk , 25 (1970) pp. 53–62
[7]	M.L. Gromov, "Isometric imbeddings and immersions" Soviet Math. Dokl. , 11 : 3 (1970) pp. 1206–1209 Dokl. Akad. Nauk SSSR , 192 (1970) pp. 794–797

Comments

The Nash theorem in differential topology says that a compact connected 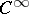-manifold without boundary is diffeomorphic to a component of a real algebraic variety.

Let 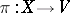be a smooth (i.e. 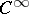-) fibration. Denote by 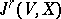the space of -jets (of germs) of smooth sections 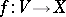(cf. Germ; Jet). The -th order jet of a section 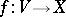is denoted by 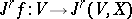. A section 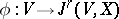is called holonomic if there is a 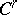-section 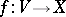such that 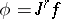; 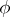determines 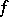uniquely (if it exists). The fine topology on the space 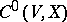of 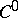-sections 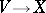is obtained by taking as a basis the subsets 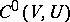where 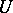runs over the open subsets of 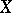. The fine 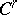-topology on 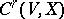is induced by the imbedding 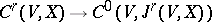, , 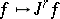from the fine 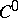-topology to .

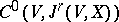The Nash approximation theorem says that an arbitrary Riemannian 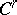-metric on 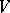has a fine 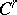-approximation by some 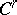-metric 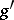on 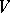that admits 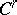-immersions 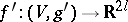for some 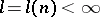, where .

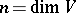The Nash–Kuiper theorem [1], [2] says that an arbitrary differentiable immersion 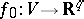for 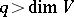admits a 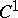-continuous homotopy of immersions 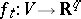, , 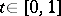to an isometric immersion .

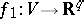References

[a1]	M.W. Hirsch, "Differential topology" , Springer (1976)
[a2]	M. Gromov, "Partial differential relations" , Springer (1986) (Translated from Russian)