Helicoid

A ruled surface described by a straight line that rotates at a constant angular rate around a fixed axis, intersects the axis at a constant angle 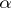, and at the same time becomes gradually displaced at a constant rate along this axis.

Figure: h046880a

If 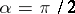, the helicoid is called straight or right (cf. Fig.); if 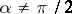, it is called oblique. The equation of a helicoid in parametric form is

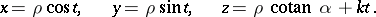Comments

Every straight helicoid is a minimal surface (it is then sometimes called minimal). See [a2], [a1]. Moreover, a ruled surface which is minimal is necessarily a part of a right helicoid.

References

[a1]	M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1975) pp. 214
[a2]	M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 218–219
[a3]	B. O'Neill, "Elementary differential geometry" , Acad. Press (1966)
[a4]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)