Lattice of points
point lattice, in 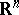 , with basis
, with basis 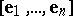
The set  of points
of points  , where
, where 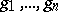 are integers.
are integers.
The lattice 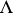 can be regarded as the free Abelian group with
can be regarded as the free Abelian group with  generators. A lattice
generators. A lattice  has an infinite number of bases; their general form is
has an infinite number of bases; their general form is 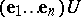 , where
, where 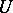 runs through all integral matrices of determinant
runs through all integral matrices of determinant 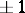 . The quantity
. The quantity
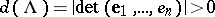 |
is the volume of the parallelopipedon formed by the vectors  . It does not depend on the choice of a basis and is called the determinant of the lattice
. It does not depend on the choice of a basis and is called the determinant of the lattice 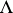 .
.
The partition of point lattices into Voronoi lattice types plays an important role in the geometry of quadratic forms (cf. Quadratic form).
Comments
The idea of lattices and lattice points links geometry to arithmetic (integers). Therefore it plays a central role in the geometry of numbers; integer programming (lattice point theorems); Diophantine approximations; reduction theory; analytic number theory; numerical analysis; crystallography (cf. Crystallography, mathematical); coding and decoding; combinatorics; geometric algorithms, and other areas.
References
| [a1] | J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1972) |
| [a2] | P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989) |
| [a3] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) |
| [a4] | P.M. Gruber (ed.) J.M. Wills (ed.) , Handbook of convex geometry , North-Holland (1992) |
| [a5] | R. Kannan, L. Lovasz, "Covering minima and lattice-point-free convex bodies" Ann. of Math. , 128 (1988) pp. 577–602 |
Lattice of points. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lattice_of_points&oldid=24096