Fréchet derivative
strong derivative
The most widespread (together with the Gâteaux derivative, which is sometimes called the weak derivative) derivative of a functional or a mapping. The Fréchet derivative of a mapping 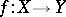 of a normed space
of a normed space 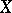 into a normed space
into a normed space 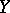 at a point
at a point 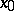 is the linear continuous operator
is the linear continuous operator 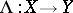 satisfying the condition
satisfying the condition
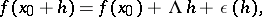 |
where
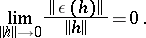 |
The operator 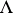 satisfying these conditions is unique (if it exists) and is denoted by
satisfying these conditions is unique (if it exists) and is denoted by 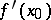 ; the linear mapping
; the linear mapping 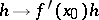 is called the Fréchet differential. If
is called the Fréchet differential. If 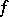 has a Fréchet derivative at
has a Fréchet derivative at 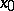 , it is said to be Fréchet differentiable. The most important theorems of differential calculus hold for Fréchet derivatives — the theorem on the differentiation of a composite function and the mean value theorem. If
, it is said to be Fréchet differentiable. The most important theorems of differential calculus hold for Fréchet derivatives — the theorem on the differentiation of a composite function and the mean value theorem. If 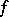 is continuously Fréchet differentiable in a neighbourhood of a point
is continuously Fréchet differentiable in a neighbourhood of a point 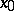 and if the Fréchet derivative
and if the Fréchet derivative 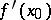 at
at 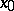 is a homeomorphism of the Banach spaces
is a homeomorphism of the Banach spaces 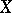 and
and 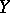 , then the inverse mapping theorem holds. See also Differentiation of a mapping.
, then the inverse mapping theorem holds. See also Differentiation of a mapping.
Comments
References
| [a1] | M.S. Berger, "Nonlinearity and functional analysis" , Acad. Press (1977) |
Fréchet derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9chet_derivative&oldid=23280