Packing

of a finite (or infinite) family of sets 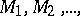in a set

Fulfillment of the conditions

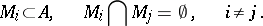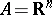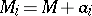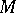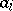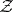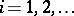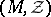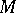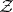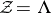In the geometry of numbers usually , , where is a given set and the range over a certain set of vectors in (); in this case one speaks of the packing of the set by the system of vectors . If is a point lattice in , one speaks of a lattice packing .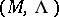

One also considers packing of sets 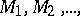not only in 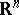but also in other manifolds, on an -dimensional sphere, in a given domain, etc. (cf. [1], [2]). Sometimes a packing is defined as a system of (for example, closed domains) 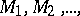which do not meet in interior points (cf. [1]).

References

[1]	E.P. Baranovskii, "Packings, coverings, partitions, and certain other distributions in spaces of constant curvature" Progress in Math. , 9 (1971) pp. 209–253 Itogi Nauk. Algebra. Topol. Geom. 1967 (1969) pp. 181–225
[2]	L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972)
[3]	C.A. Rogers, "Packing and covering" , Cambridge Univ. Press (1964)

Comments

Sphere packing has various applications in error-correcting codes (cf. Error-correcting code), the channel coding problem, Steiner systems (cf. Steiner system), -designs, and in the theory of finite groups. The most important special case is the sphere packing in 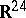via the Leech lattice. Finite and infinite sphere packing in 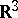has applications in classical and modern crystallography (cf. Crystallography, mathematical).

A packing in 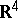which is also a covering in 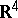(cf. Covering and packing; Covering (of a set)) is called a tiling or tesselation. In other words: A tiling is a countable family of closed sets which cover 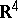without gaps or overlaps. The sets are called tiles. If all sets are congruent, they are the copies of a prototile.

In the geometry of numbers, lattice tilings are of interest; there are tilings of the form 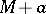, , 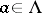where 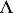is a lattice of points. For an exhaustive account of planar tilings see [a3]. Higher-dimensional results and, in particular, relations to crystallography are treated in [a2], [a1]. Classical types of tilings are Dirichlet–Voronoi tilings and Delone triangulations or 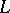-partitions, see [a1] and Voronoi lattice types.

References

[a1]	P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989)
[a2]	P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint)
[a3]	B. Grünbaum, G.C. Shephard, "Tilings and patterns" , Freeman (1986)
[a4]	J.H. Conway, N.J.A. Sloane, "Sphere packing, lattices and groups" , Springer (1988)